Bias-Variance Tradeoff

方差 varinace

代表我们使用不同训练集时模型表现的差异如果模型具有较大的方差，训练集只要有少许变化，模型会有很大的改变。复杂的模型一般具有更大的方差（方差小模型泛化能力强）test set 和 train set 的差多少
偏差 bias

代表实际模型与理想模型的差别 (偏差小模型拟合能力强) 在train set的错误率

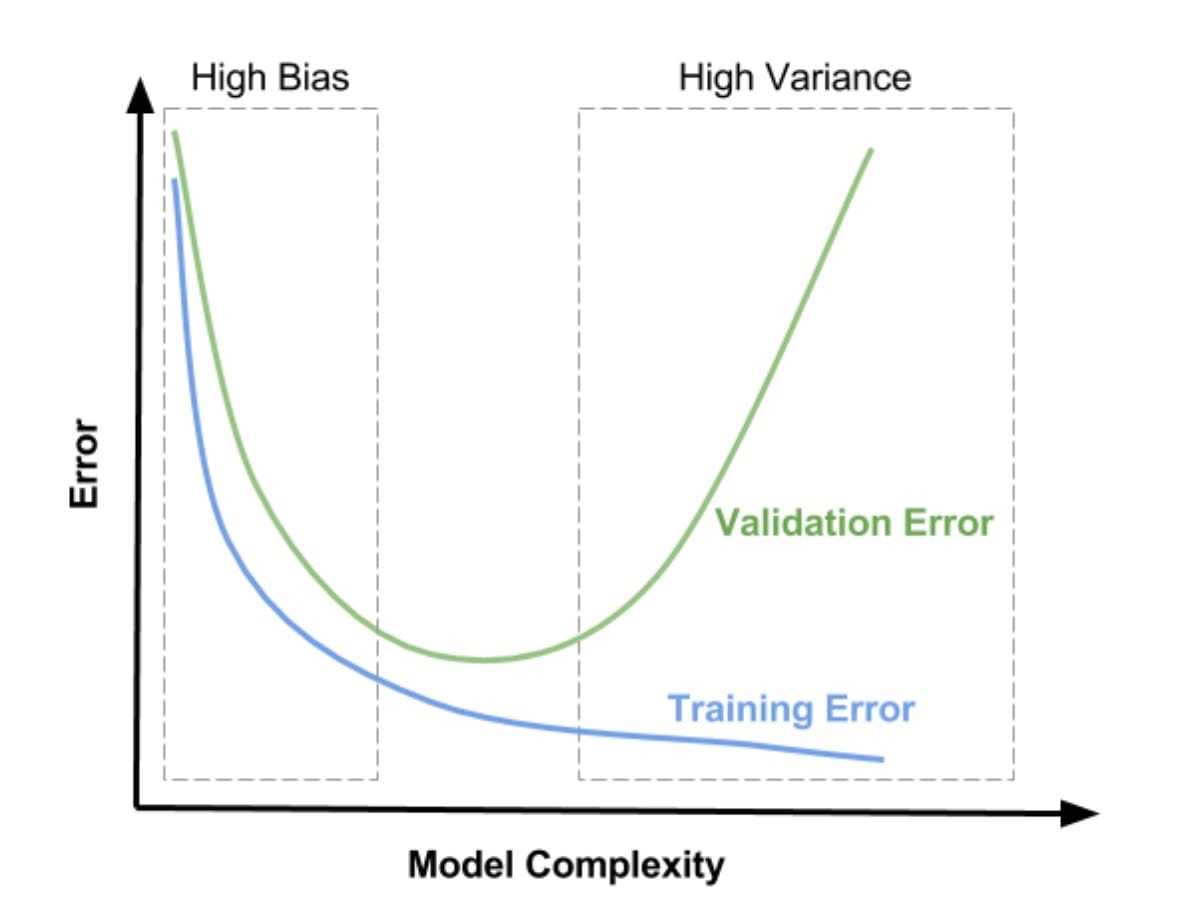
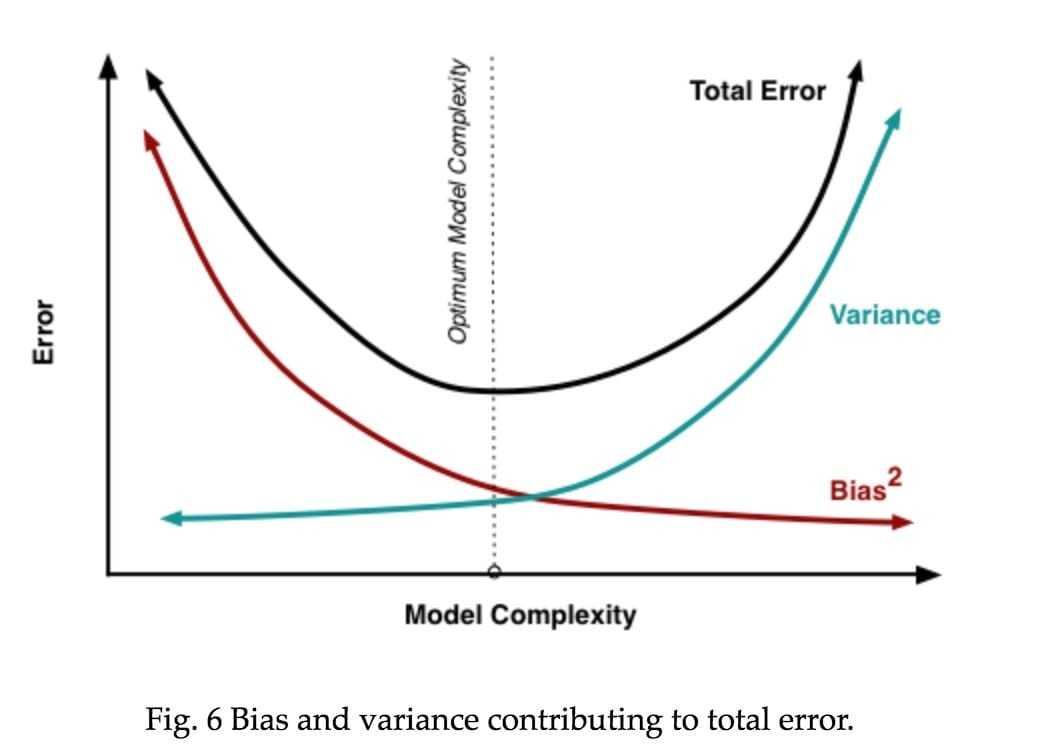
过拟合

主要原因

noise
模型复杂度太高
train-set too small

解决

数据清洗（错误数据的更正，或者删除）
简化模型
更多数据（如果没有办法获得更多的训练集，对已知的样本进行简单的处理、变换，从而获得更多的样本）
regularization
减少特征
validation

维度灾难

当模型很复杂的时候，复杂度本身就会引入一种noise，所以即使高阶无noise，模型也不能很好泛化。

欠拟合

增加模型的迭代次数
生成更好特征供训练使用
降低正则化水平

Regularization

正则化给予model惩罚 减低model复杂度

Validation

普通

set 分train and test => Modelargmin(E_test) => 得到model再用整体数据集训练分量4:1

Leave-One-Out

每次从数据集中取一个样本作为test-set，直到N个样本都作过验证集，共计算N次，最后对验证误差求平均

计算量大稳定性，例如对于二分类问题，取值只有0和1两种，预测本身存在不稳定的因素，那么对所有的Eloocv计算平均值可能会带来很大的数值跳动所以Leave-One-Out方法在实际中并不常用

V-Fold Cross Validation

Leave-One-Out是将N个数据分成N分，那么改进措施是将N个数据分成V份（例如V=10），计算过程与Leave-One-Out相似。这样可以减少总的计算量，又能进行交叉验证，这种方法称为V-折交叉验证。Leave-One-Out就是V-折交叉验证的一个极端例子

example

cross_val_score K-fold cross-validation

from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")

归一化

原始数据进行线性变换把数据映射到[0,1] 最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景。

\[\text{x'=}\frac{x-min}{max-min}\]

标准化

数据均值为0，标准差为1 其中μ是样本的均值，σ是样本的标准差在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景

\[x'=\frac{x-\mu}\sigma\]

如果想保留原始数据中由标准差所反映的潜在权重关系应该选择归一化

非线性变换

用不太复杂的model 解决非线性问题 通过非线性变换，将非线性模型映射到另一个空间，转换为线性模型，再来进行线性分类

特征转换
训练线性模型

例如

模型太复杂容易带来过拟合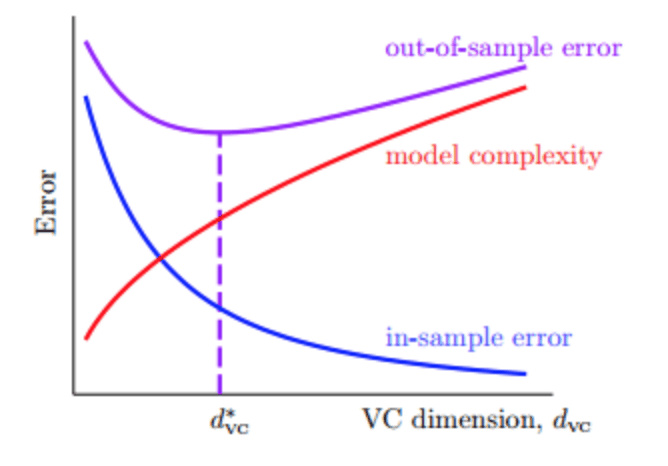非线性变换可能会带来的一些问题：时间复杂度和空间复杂度的增加，尽可能使用简单的模型，而不是模型越复杂越好

Bias-Variance trick