Hyperparameters Tuning

常见超参数

$\alpha$：学习因子
$\beta$：动量梯度下降因子
$\beta_1,\beta_2,\varepsilon$：Adam算法参数
layers：神经网络层数
hidden units：各隐藏层神经元个数
active function：激活函数
learning rate decay：学习因子下降参数
mini-batch size：批量训练样本包含的样本个数

参数采样

随机采样
放大表现较好的区域，再对此区域做更密集的随机采样，由粗到细的采样（coarse to fine sampling scheme）

为超参数选择合适的范围

对于某些超参数，可能需要非均匀随机采样（即非均匀刻度尺）。例如超参数αα\alpha，待调范围是[0.0001, 1]。如果使用均匀随机采样，那么有90%的采样点分布在[0.1, 1]之间，只有10%分布在[0.0001, 0.1]之间。这在实际应用中是不太好的，因为最佳的$\alpha$值可能主要分布在[0.0001, 0.1]之间，而[0.1, 1]范围内$\alpha$值效果并不好。因此我们更关注的是区间[0.0001, 0.1]，应该在这个区间内细分更多刻度。

将linear scale转换为log scale，将均匀尺度转化为非均匀尺度，然后再在log scale下进行均匀采样。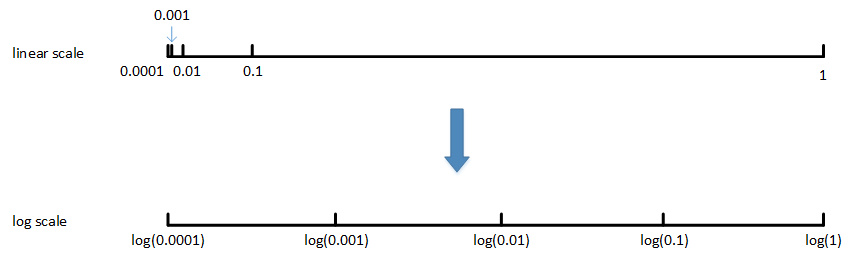一般解法是，如果线性区间为[a, b]，令m=log(a)，n=log(b)，则对应的log区间为[m,n]。对log区间的[m,n]进行随机均匀采样，然后得到的采样值r，最后反推到线性区间，即$10^r$。$10^r$就是最终采样的超参数。

m = np.log10(a)
n = np.log10(b)
r = np.random.rand()
r = m + (n-m)*r
r = np.power(10,r)

经过调试选择完最佳的超参数并不是一成不变的，一段时间之后（例如一个月），需要根据新的数据和实际情况，再次调试超参数，以获得实时的最佳模型。

一般来说，对于非常复杂或者数据量很大的模型,一个模型进行训练，调试不同的超参数。也可以对多个模型同时进行训练，每个模型上调试不同的超参数，根据表现情况，选择最佳的模型。