Recurrent Neural Networks 循环神经网络
应用领域
语音识别,情感分类,机器翻译
Notation
符号


Recurrent Neural Network Model
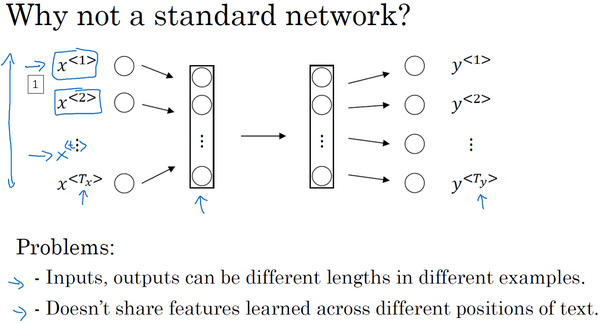
- 不同样本的输入序列长度或输出序列长度不同,即$T_x^{(i)}\neq T_x^{(j)}$,$T_y^{(i)}\neq T_y^{(j)}$,造成模型难以统一。 解决办法之一是设定一个最大序列长度,对每个输入和输出序列补零并统一到最大长度。但是这种做法实际效果并不理想。
- 这种标准神经网络结构无法共享序列不同\(x^{<t>}\)之间的特征。例如,如果某个\(x^{<t>}\)即“Harry”是人名成分,那么句子其它位置出现了“Harry”, 也很可能也是人名。这是共享特征的结果,如同CNN网络特点一样。但是,上图所示的网络不具备共享特征的能力。 值得一提的是,共享特征还有助于减少神经网络中的参数数量,一定程度上减小了模型的计算复杂度。
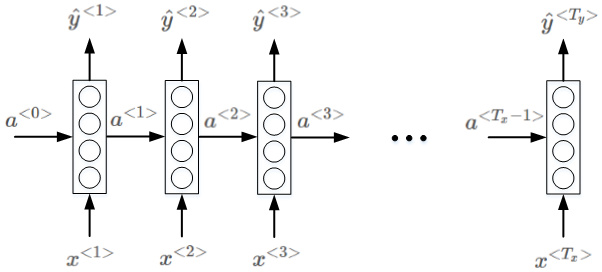
序列模型从左到右,依次传递,此例中,$T_x=T_y$。会传入到第t+1个元素中,作为输入。其中,一般为零向量。
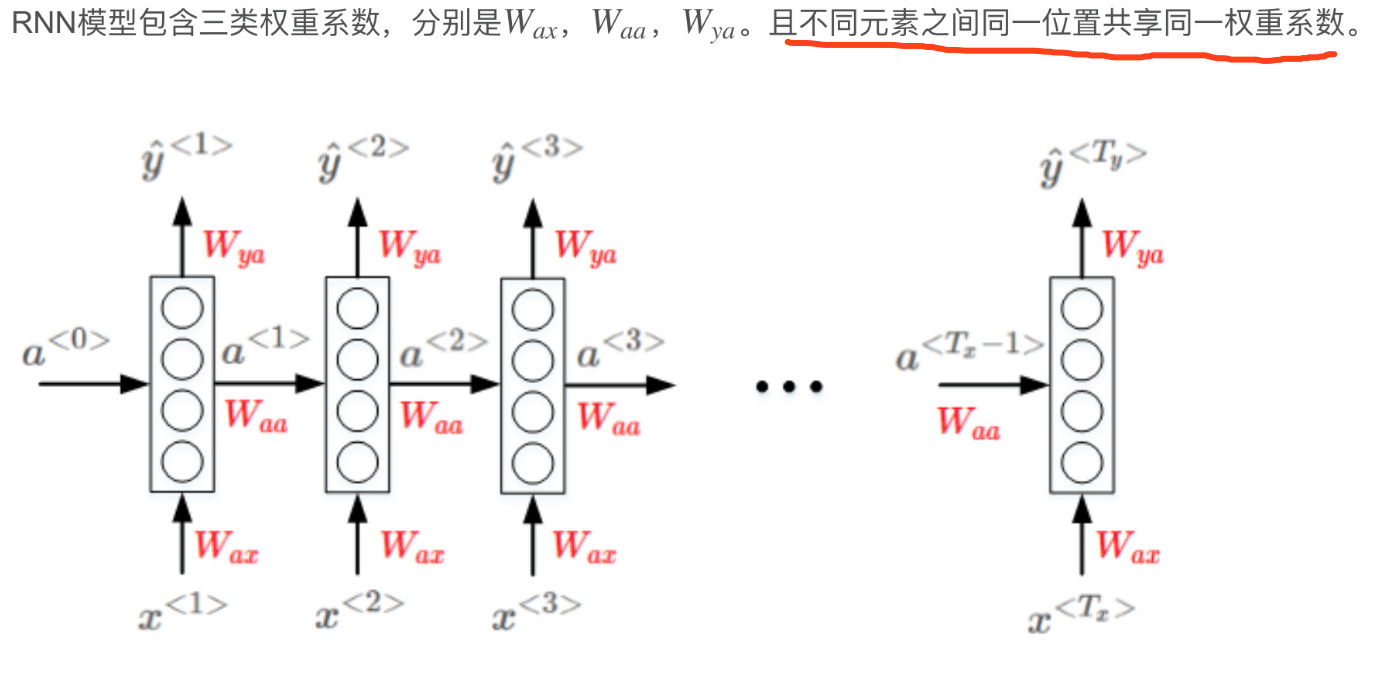
RNN的正向传播(Forward Propagation)过程为:
\[a^{<t>}=g(W_{aa}\cdot a^{<t-1>}+W_{ax}\cdot x^{<t>}+ba)\] \[\hat y^{<t>}=g(W_{ya}\cdot a^{<t>}+b_y)\]其中,$g(\cdot)$表示激活函数,不同的问题需要使用不同的激活函数。
简化为:
\[a^{<t>}=g(W_a[a^{<t-1>},x^{<t>}]+b_a)\] \[\hat y^{<t>}=g(W_{y}\cdot a^{<t>}+b_y)\]Backpropagation
针对上面识别人名的例子,经过RNN正向传播,单个元素的Loss function为:
\[L^{<t>}(\hat y^{<t>},y^{<t>})=-y^{<t>}log\ \hat y^{<t>}-(1-y^{<t>})log\ (1-\hat y^{<t>})\]该样本所有元素的Loss function为:
\[L(\hat y,y)=\sum_{t=1}^{T_y}L^{<t>}(\hat y^{<t>},y^{<t>})\]然后,反向传播(Backpropagation)过程就是从右到左分别计算$L(\hat y,y)$对参数$W_{a},W_{y},b_a,b_y$
Different types of RNNs
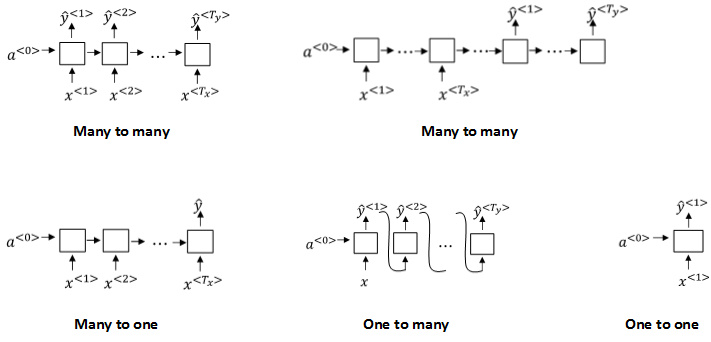
RNN模型包含以下几个类型:
- Many to many: $T_x=T_y$ seq to seq
- Many to many: $T_x\neq T_y$
- Many to one: $T_x>1,T_y=1$
- One to many: $T_x=1,T_y>1$
- One to one: $T_x=1,T_y=1$
1 | |
相同模型
static_rnn()函数为每个输入调用单元工厂的__call __()函数,创建单元的两个副本(每个单元包含 5 个循环神经元的循环层), 并具有共享的权重和偏置项,像前面一样。
static_rnn()函数返回两个对象。 第一个是包含每个时间步的输出张量的 Python 列表。 第二个是包含网络最终状态的张量。 当你使用基本的单元时,最后的状态就等于最后的输出。
1 | |
缺点 这种方法仍然会建立一个每个时间步包含一个单元的图。如果使用具有200个时间步长的输入进行调用, 则创建一个具有200个RNN步长的静态图形。首先,图形创建很慢。其次,您无法传递比您最初指定的更长的序列(> 200)。
tf.nn.dynamic_rnn解决了这个问题。它使用tf.While循环在执行时动态构造图形。这意味着图表创建速度更快,您可以提供可变大小的批量。
1 | |
变长输入序列
你应该在调用dynamic_rnn()(或static_rnn())函数时设置sequence_length参数
1 | |
action
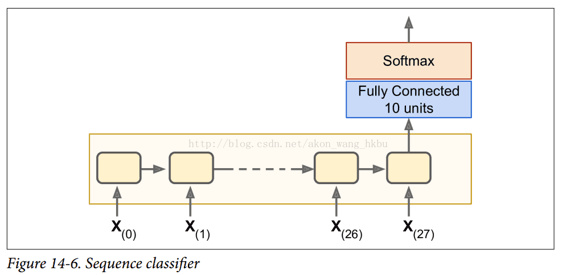
1 | |
NLP
如何使用RNN构建语言模型
大量的单词语句语料库(corpus)构成足够大的训练集,对corpus的每句话进行切分词(tokenize),建立vocabulary,对每个单词进行one-hot编码。
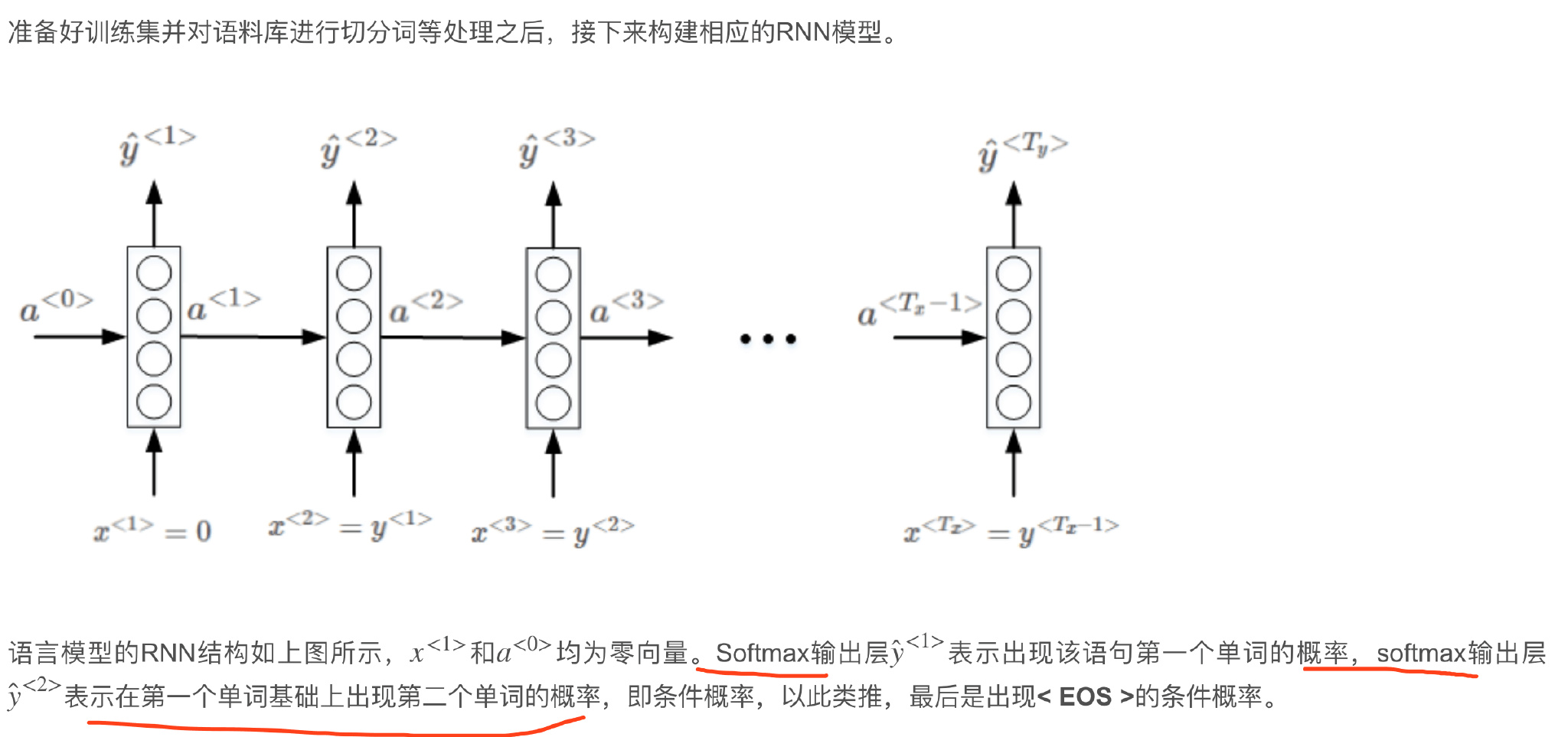 对语料库的每条语句进行RNN模型训练,最终得到的模型可以根据给出语句的前几个单词预测其余部分,将语句补充完整。
对语料库的每条语句进行RNN模型训练,最终得到的模型可以根据给出语句的前几个单词预测其余部分,将语句补充完整。
循环神经网络的梯度消失(Vanishing gradients with RNNs)
某个word可能与它距离较远的某个word具有强依赖关系。
 一般的RNN模型每个元素受其周围附近的影响较大,难以建立跨度较大的依赖性。上面两句话的这种依赖关系,
由于跨度很大,普通的RNN网络容易出现梯度消失,捕捉不到它们之间的依赖,造成语法错误。
一般的RNN模型每个元素受其周围附近的影响较大,难以建立跨度较大的依赖性。上面两句话的这种依赖关系,
由于跨度很大,普通的RNN网络容易出现梯度消失,捕捉不到它们之间的依赖,造成语法错误。
RNN也可能出现梯度爆炸的问题,即gradient过大。常用的解决办法是设定一个阈值, 一旦梯度最大值达到这个阈值,就对整个梯度向量进行尺度缩小。这种做法被称为gradient clipping。
GRU单元(Gated Recurrent Unit(GRU))
更好地捕捉深层连接,并改善了梯度消失问题
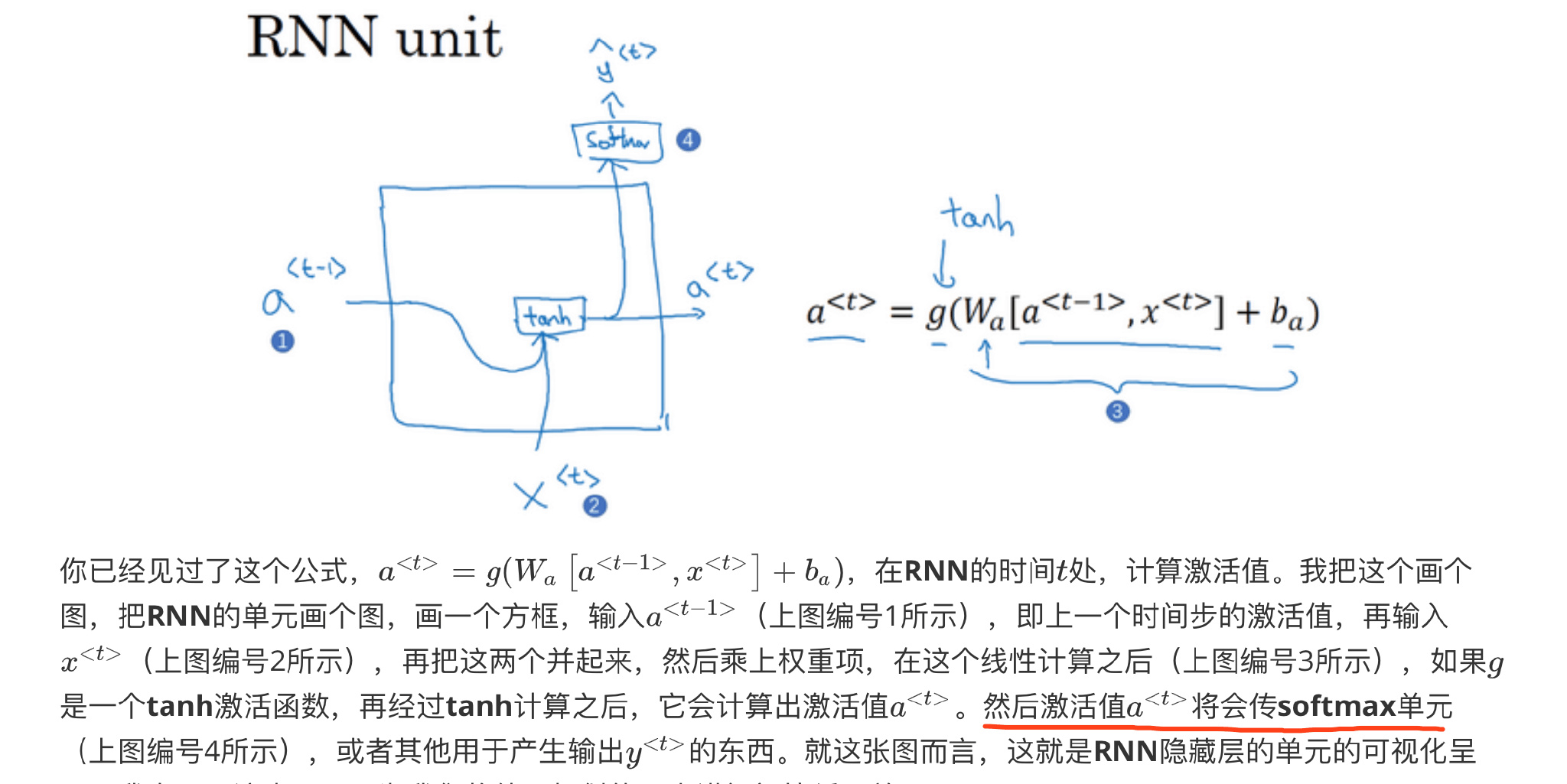 为了解决梯度消失问题,对上述单元进行修改,添加了记忆单元,构建GRU(门控循环单元)
为了解决梯度消失问题,对上述单元进行修改,添加了记忆单元,构建GRU(门控循环单元)
GRU单元将会有个新的变量称为c,代表细胞(cell),记忆细胞的作用是提供了记忆的能力。 \(我们将用一个候选值重写记忆细胞,即{\tilde{c}}^{<t>}的值,所以它就是个候选值,替代了c^{<t>}的值。\) \(GRU中真正重要的思想是我们有一个门,我先把这个门叫做\Gamma_u,这是个下标为u的大写希腊字母\Gamma,u代表更新门,这是一个0到1之间的值。\)
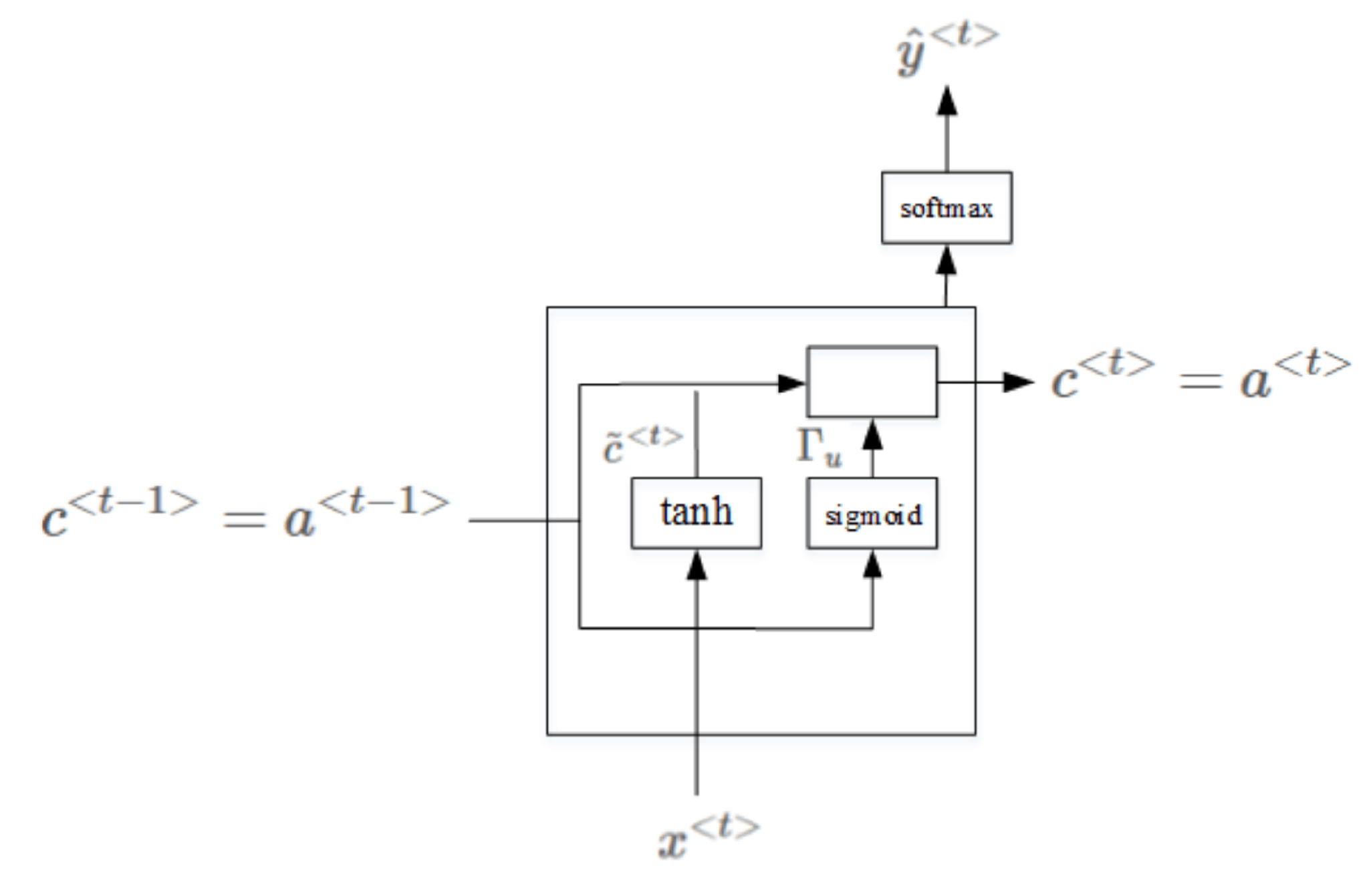
 \(如果这个更新值\Gamma_{u} =1,也就是说把这个新值,即c^{<t>}设为候选值,c^{<t>} = {\tilde{c}}^{<t>}。\)
\(如果\Gamma_{u}= 0,意思就是说不更新它,就用旧的值。c^{<t>} =c^{<t-1>}。\)
\(如果这个更新值\Gamma_{u} =1,也就是说把这个新值,即c^{<t>}设为候选值,c^{<t>} = {\tilde{c}}^{<t>}。\)
\(如果\Gamma_{u}= 0,意思就是说不更新它,就用旧的值。c^{<t>} =c^{<t-1>}。\)
这就是GRU单元或者说是一个简化过的GRU单元,它的优点就是通过门决定,当你从左到右扫描一个句子的时候, 这个时机是要更新某个记忆细胞,还是不更新,不更新直到你到你真的需要使用记忆细胞的时候,这可能在句子之前就决定了。 因为sigmoid的值,现在因为门很容易取到0值,只要这个值是一个很大的负数,再由于数值上的四舍五入,上面这些门大体上就是0,或者说非常非常非常接近0。 所以在这样的情况下,这非常有利于维持细胞的值。因为$\Gamma_{u}$很接近0,可能是0.000001或者更小,这就不会有梯度消失的问题了。 因为$\Gamma_{u}$很接近0,这就是说$c^t$几乎就等于$c^{t-1}$,而且$c^t$的值也很好地被维持了, 即使经过很多很多的时间步。这就是缓解梯度消失问题的关键,因此允许神经网络运行在非常庞大的依赖词上,比如说cat和was单词即使被中间的很多单词分割开。
上面介绍的是简化的GRU模型,完整的GRU添加了另外一个gate,即$\Gamma_r$,表达式如下: \(r代表相关性(**relevance**)。这个\Gamma_{r}门告诉你计算出的下一个c^{<t>}的候选值{\tilde{c}}^{<t>}跟c^{<t-1>}有多大的相关性。\)
\[\tilde c^{<t>}=tanh(W_c[\Gamma_r*c^{<t-1>},x^{<t>}]+b_c)\] \[\Gamma_u=\sigma(W_u[c^{<t-1>},x^{<t>}]+b_u)\] \[\Gamma_r=\sigma(W_r[c^{<t-1>},x^{<t>}]+b_r)\] \[c^{<t>}=\Gamma_u*\tilde c^{<t>}+(1-\Gamma_u)*c^{<t-1>}\] \[a^{<t>}=c^{<t>}\]LSTM
长短期记忆 long short term memory
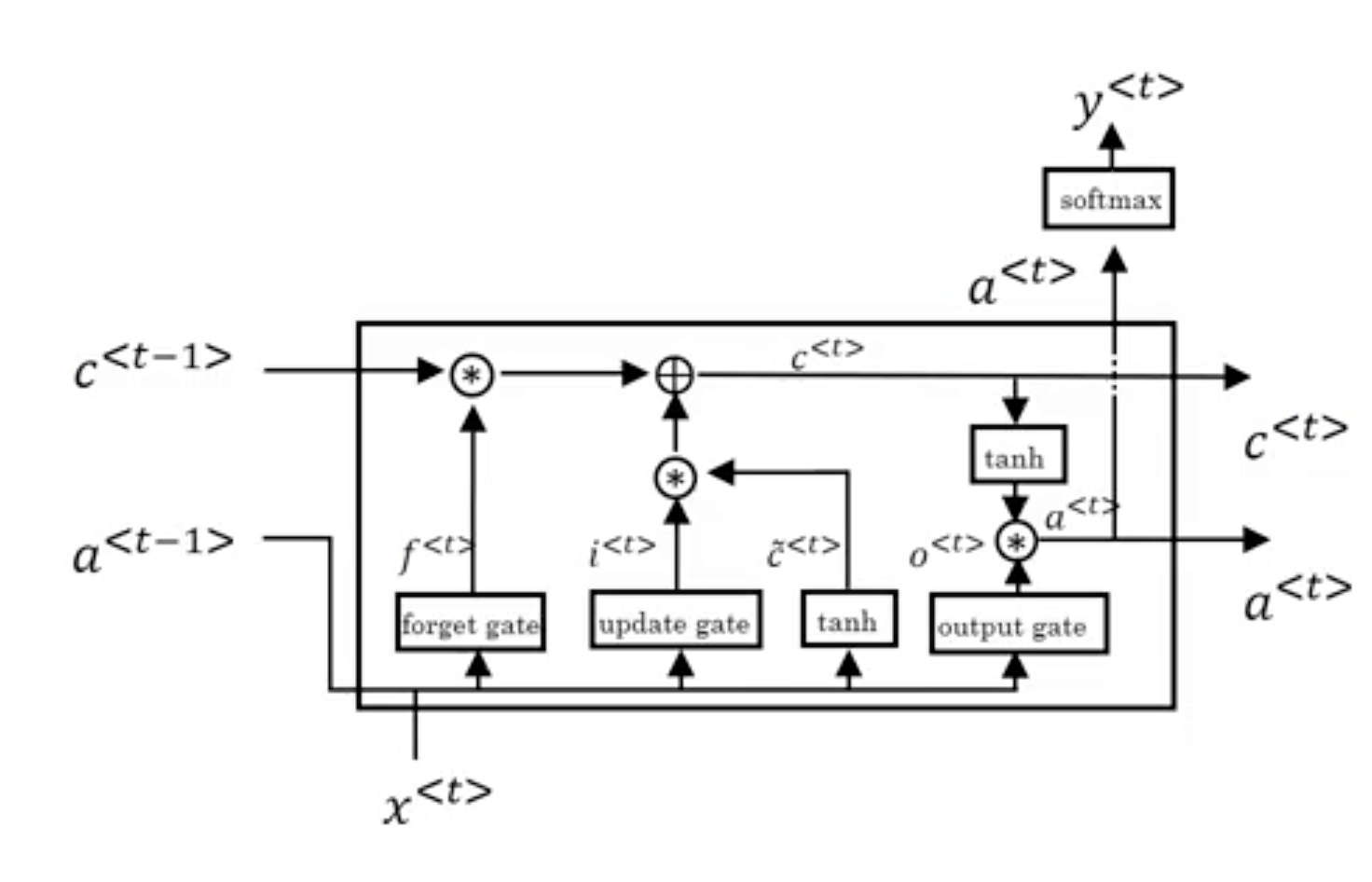
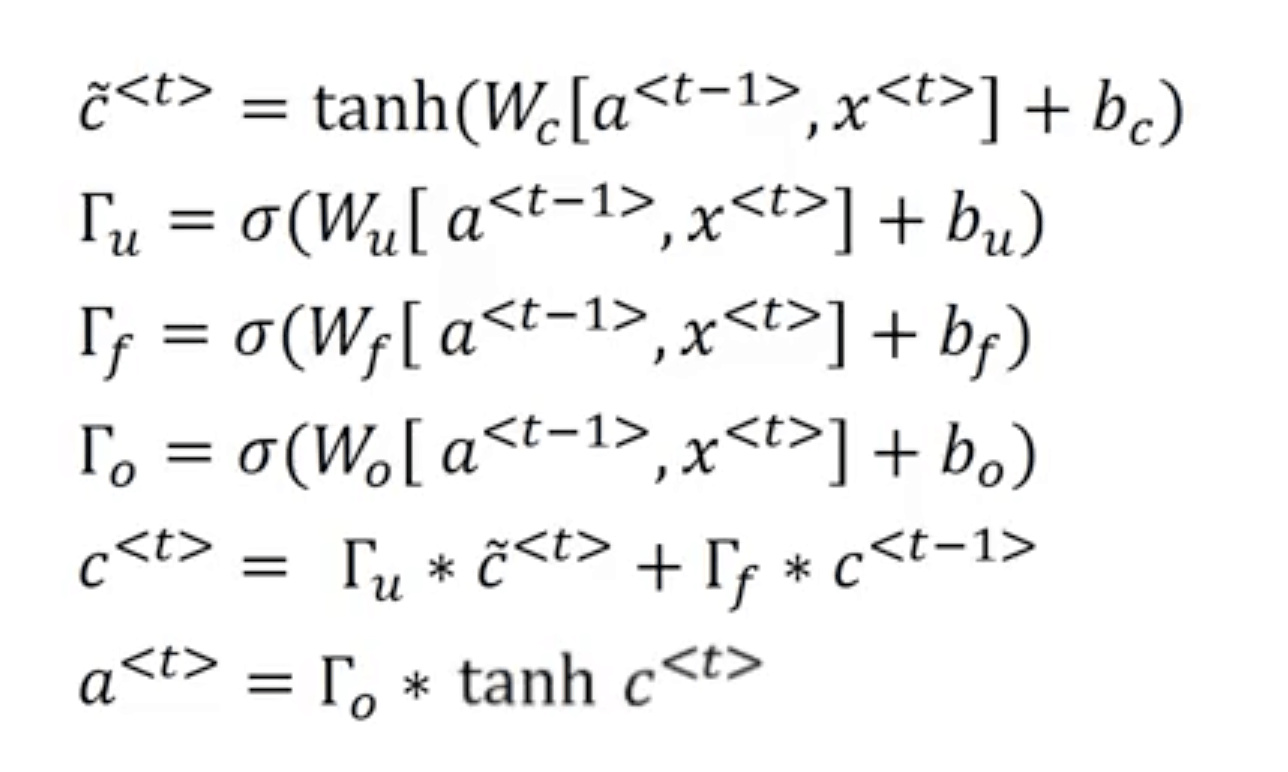 LSTM包含三个gates:Γu,Γf,Γo,分别对应update gate,forget gate和output gate。
LSTM包含三个gates:Γu,Γf,Γo,分别对应update gate,forget gate和output gate。
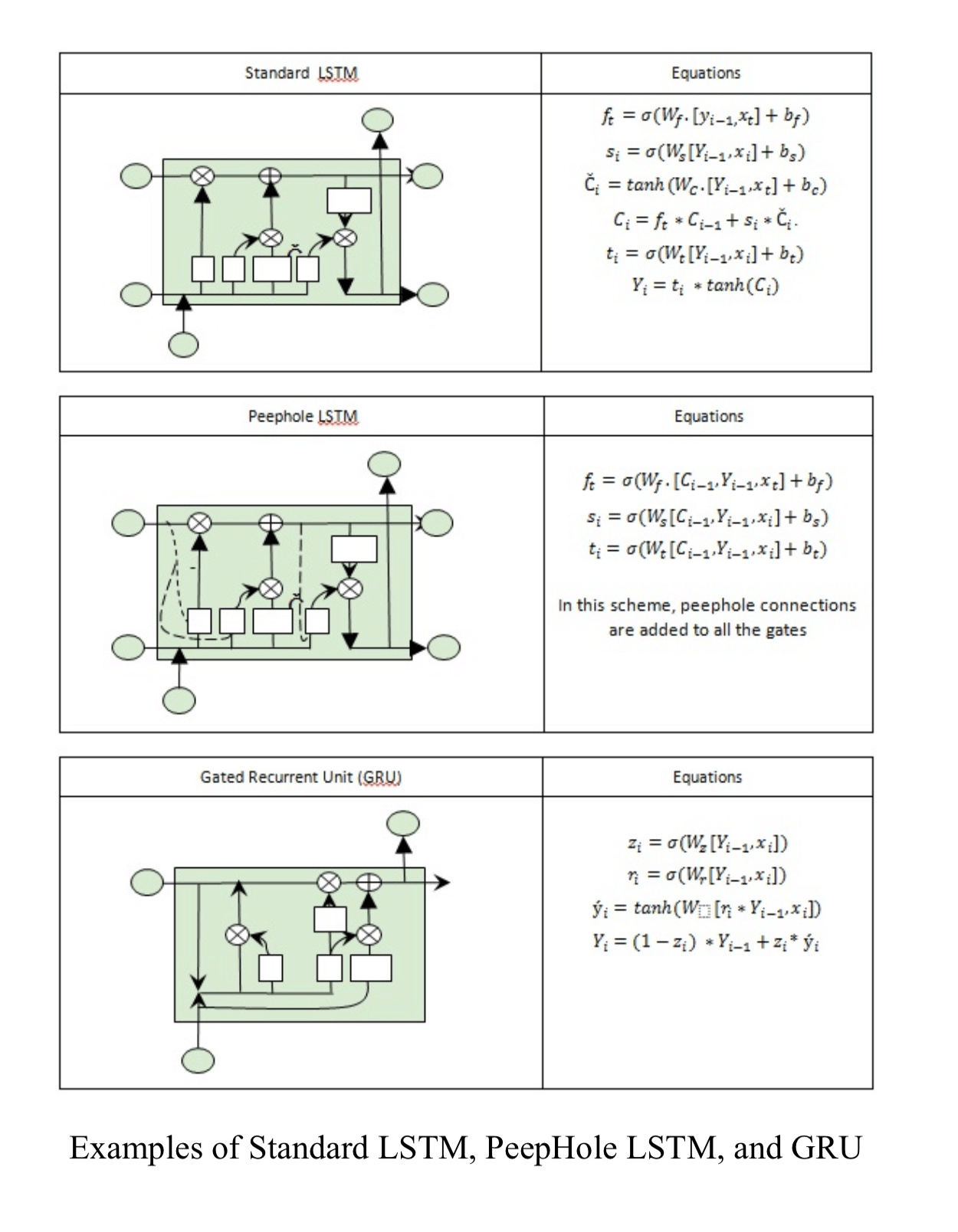
\(peephole connection(窥视孔连接)其实意思就是门值不仅取决于a^{<t-1>}和x^{<t>}, 也取决于上一个记忆细胞的值(c^{<t-1>}),\) \(然后peephole connection就可以结合这三个门(\Gamma_{u}、\Gamma_{f}、\Gamma_{o})来计算了。\)
1 | |
Bidirectional RNN
- 在序列的某点处不仅可以获取之前的信息,还可以获取未来的信息。
- 深层的RNN
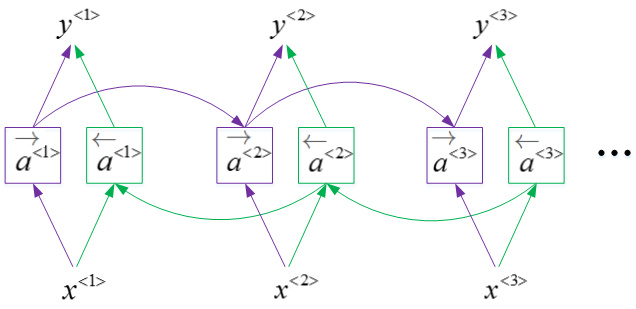 双向循环神经网络,并且这些基本单元不仅仅是标准RNN单元,也可以是GRU单元或者LSTM单元。
事实上,很多的NLP问题,对于大量有自然语言处理问题的文本,有LSTM单元的双向RNN模型是用的最多的。
所以如果有NLP问题,并且文本句子都是完整的,首先需要标定这些句子,一个有LSTM单元的双向RNN模型,有前向和反向过程是一个不错的首选。
双向循环神经网络,并且这些基本单元不仅仅是标准RNN单元,也可以是GRU单元或者LSTM单元。
事实上,很多的NLP问题,对于大量有自然语言处理问题的文本,有LSTM单元的双向RNN模型是用的最多的。
所以如果有NLP问题,并且文本句子都是完整的,首先需要标定这些句子,一个有LSTM单元的双向RNN模型,有前向和反向过程是一个不错的首选。
缺点:
- 需要完整的数据的序列,才能预测任意位置。
Deep RNN
深层循环神经网络
RNN的多个层堆叠在一起构建更深的模型
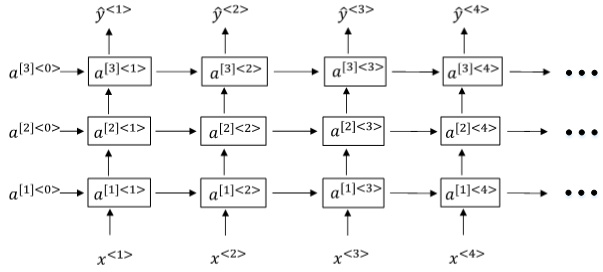 与DNN一样,用上标[l]表示层数。Deep RNNs中\(a^{[l]<t>}\)的表达式为:
与DNN一样,用上标[l]表示层数。Deep RNNs中\(a^{[l]<t>}\)的表达式为:
我们知道DNN层数可达100多,而Deep RNNs一般没有那么多层,3层RNNs已经较复杂了。
1 | |
states 变量包含了每层的一个张量,这个张量就代表了该层神经单元的最终状态(维度为[batch_size, n_neurons])