- 状态转移概率
- 状态数量
- 初始位置概率
马尔科夫链Markov Chain
描述离散状态之间在不同时刻的转移关系
假设
- t+m 时刻系统状态的概率分布只与t时刻的状态有关，与t时刻以前的状态无关 （m阶Markov Chain 简化m=1 ）
- 状态转移概率 与 t 无关
一个马尔可夫链模型可表示为=(S，P，Q)
- S是系统所有可能的状态所组成的非空的状态集
- P是状态转移矩阵 $P_{kl\;}=\;P(X_t\;=\;S_l\vert X_{t-m}\;=\;S_k)$ t 时刻从k状态转移到l状态的概率
- Q初始概率分布
隐马尔科夫 Hide Markov Model HMM
在状态 State的基础上加入Token概念，每个状态以不同的概率产生一组可观察的Token => 生成概率（Emission Probability）
HMM里面State是不可见的，只能观察Token
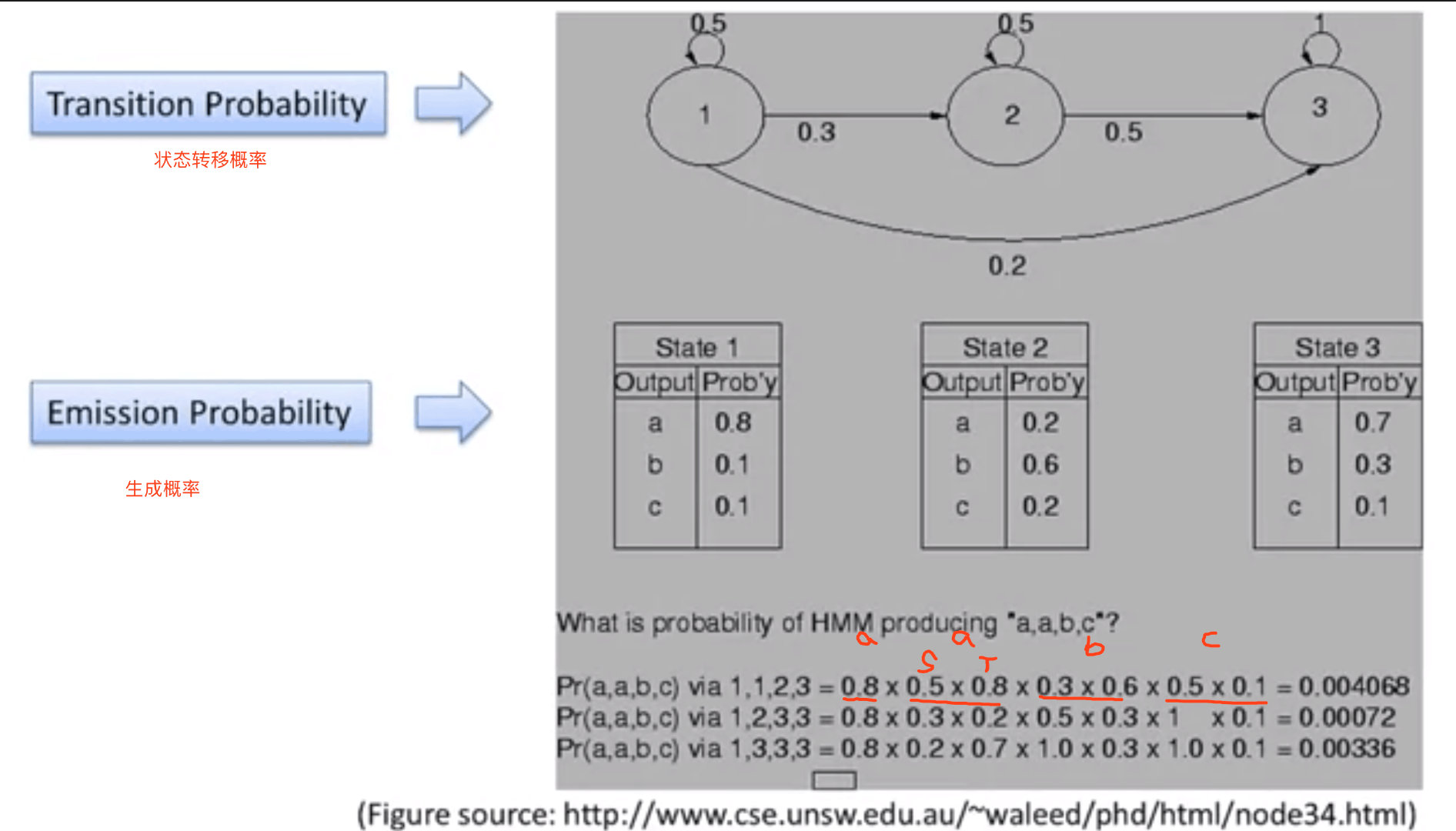同一个Token序列有不同State路径 argmaxP(S|T)
- token 反推state 选概率大