向量索引

发表于 | 分类于 | 阅读次数

向量数据库

与传统数据库区别

  • 传统数据库:1)关系型数据库;2) 非关系型 NoSQL 数据库;3)分析型数据库。
  • 搜索方式:索引(B-Tree、倒排等) + 排序算法(BM25、TF-IDF)实现。

  • 搜索本质:基于文本的精确匹配， SQL 语言进行精确匹配与查找，输出符合查询条件数据

  • 适合场景:关键字搜索功能较优，对于语义搜索功能较差。

差异点

  • 传统数据库:归结为点查和范围查(精确查找)，查询得到结果为符合条件/不符合条件
  • 向量数据库:针对向量近似查找，查询得到结果是与输入条件相似 TOP-K 向量
  • 传统数据库:直接处理数据，即使用 SQL 语言对文本精确匹配与查找，输出符合查询条件数据
  • 向量数据库:将非结构化数据转化为向量，再基于向量数据库中进行存储、计算和建立索引

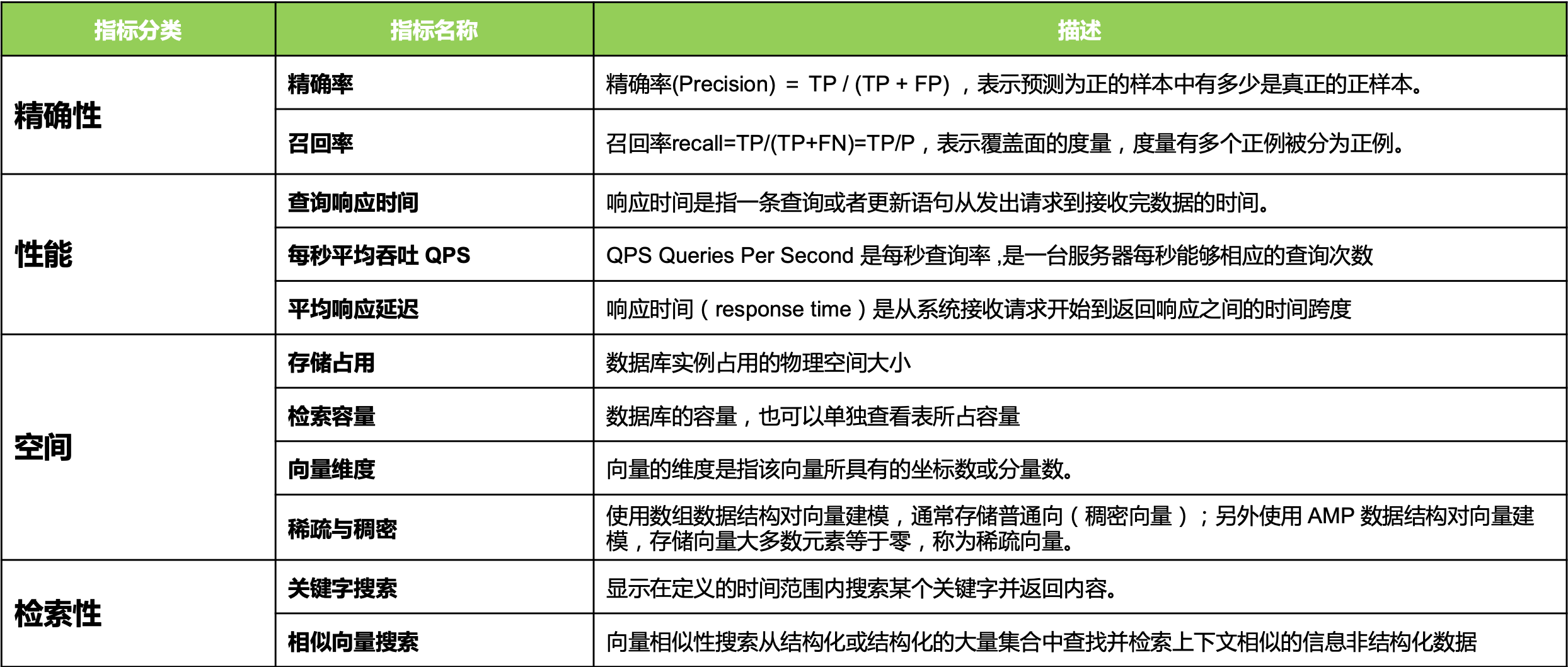
常用评价标准

  • 准确率 =检索相关的向量/检索出的向量总数
  • 召回率=检索相关的向量/向量数据库中相关的向量总数
  • QPS 每秒向量数据库能够处理的查询请求次数
  • 平均响应延迟 向量数据库的请求平均响应时间

embedding 向量化 数学向量，也叫特征向量 是一个浮点数或二进制数的数组，通过对非结构化数据转换为具体的 vector(对非结构化数据的特征抽 象) ，计算两个向量距离来判断其相似度

混合搜索系统

  • Key Word搜索:当用户知道期望搜索的结果或者与搜索词中的短语完全匹配时，找到明确相 关、有用的结果，使用传统数据库，而非向量数据库
  • 向量搜索：当用户不知道需要明确的搜索目标，而是期望搜索语义相关、特征相关结果。使用向量数据库，而非传统数据库。
  • 混合关键字+向量搜索：结合全文关键字和向量搜索的候选结果使用交叉编码器模型对结果重新排名。结合传统数据库和向量数据库。

向量索引

In-memory Index

https://db-engines.com/en/ranking/vector+dbms

Embedding 维度足够多，理论上可以将所有 Vector 区分开来, 通过计算 Vector 间距离来判断其相似度，即相似性度量(Similarity Metrix)

搜索本质

查询向量时，与数据库中每个向量进行的比较。提高搜索效率，返回 TOPK最近邻向量。每一次相似性对比所用时间，随数据维度增加而增加。

加快搜索

  • 按索引使用数据结构:将向量组织成基于树、图等结构来缩小搜索范围。

      哈希索引 树的索引 图的索引 倒排文件索引
    原理 高维向量映射到低维空间或低维哈希码（随机投影 加快搜索速率）:尽可能保持原始相似性
    数据库中向量被多次哈希:以确保相似点更有可能发生冲突(与传统哈希相反，其目标最大限度减少冲突)
    通过哈希表或者倒排索引来存储和检索:在索引过程，查询点也 使用与索引过程中相同哈希函数，由于相似点被分配到相同哈希 桶，因此检索速度非常快
    原理:哈希函数将相似向量相同哈希值映射到桶中，通过比较哈希值判断向量间相似度。
    哈希:Hash 碰撞概率尽可能高，越相似的向量越容易碰撞，相似向量被映射到同一个桶。
    特点:性能高，每个哈希表桶向量远少于整个空间中向量数，并提供一个近似、非穷举结果。    		 建立树结构:把高维空间划分成若干个子空间或者聚类中心， 然后用树形结构来存储和检索。
    索引算法:通过二叉搜索树算法搜索，相似数据易在同一子树， 从而更快地发现近似邻居。    		 数据结构:图中节点表示向量数据，边表示数据间相似 性。
    构图方式:相似数据点更有可能通过边连接，搜索算法 以有效方式遍历图找到相似近邻。    		 倒排文件索引(IVF):将向量空间划分为多格 Voronoi 单 元，单元以与聚类相同的方式，通过建立倒排索引表，以 减少搜索空间。
    IVF 通过将整个 vector 空间拆分成 k 个子空间，并对每个子空间找到一个代表质心（centroid）。并将子空间的所有 vector points 都 match 到这个质心上。给定一个要查询的 vector，先通过和所有的质心比较找到最近的质心，然后在这个质心所代表的子空间里搜索最近的点
    算法 LSH 局部敏感哈希 Locality Sensitive Hashing
    哈希函数将相似向量相同哈希值映射到桶中，通过比较哈希值判断向量间相似度。    		 基于精确距离计算 or 近似距离计算。 HNSW
    空间换时间算法，搜索召回率和搜索速度较高，但内存开销较大。存储所有向量，还需维护多层图结构。    		 IVF
    优缺点 优点扩展到大量数据时速度非常快，
    缺点是准确性一般    		 优点对低维数据准确率较高;
    缺点无法充分捕获数据    		 优点能够在高维数据中找到近似的近邻，从而 提高搜索性能。
    缺点是构图方式复杂，影响内存效率。    		 优点是有助于设计快速缩小感兴趣相似区域的搜 索算法;
    缺点是对于海量数据，细分向量空间会变慢。
    IVF 常与乘积量化(PQ)等量化方法结合，以提 高性能。

    通常用图和IVF

  • 减少向量大小:通过降维的方式(量化)表示向量值的长度。但是会降低召回率

    • 扁平化索引 FLAT

      Flat Indexing:使用 ANN、IF 或 HNSW 等索引，直接计算査询向量与 DB 中向量之间距离。

      为了将其与量化变体区分开来，使用这种方式使用时通常称为 IVF-Flat、HNSW-Flat 等。

    • 量化索引 Quantized indexing

      量化索引:将索引算法(IVF、HNSW)与量化方法相结合，以减少内存占用并加快索引速度。

      量化分类:标量量化(Scalar Quantization，SQ)或乘积量化(Product Quantization，PQ)

      • 标量量化 SQ将向量中的浮点数转换为整数。e. g. ，神经网络模型对权重参数的量化。牺牲了计算精度来提升存储和查询效率。

      • 乘积量化 PQ考虑沿每个向量维度值分布，执行压缩和数据缩减。将较大维度向量空间分解为较小维度子空间的笛卡尔积。

        • 大规模数据集中，聚类算法最大的问题在于内存占用大:
          1. 需要保存每个向量，向量中元素是浮点数 FP
          2. 需要维护聚类中心和每个向量的聚类中心索引
        • 随维度增加数据点间距离呈指数增长，高维坐标需要更多聚类中心点将数据点分成更小簇。否 则向量和聚类中心距离过远，会降低搜索速度和质量。
          1. 高维坐标系中，容易遇到维度灾难问题怎么整?
          2. 维护数量庞大的聚类中心?

        Product Quantization (PQ) 解决以上问题。能够在高维的向量空间中，更有效地捕捉到不同维度的相似度

        • 给定一个包含 N 个总向量的数据集（设定为 d dimension）, 将每个向量分解为 M 个子向量，每个子空间的 dimension 为 d/M。这些子向量的长度不必完全相同，但实际情况下，推荐使用相同的长度（方便代码实现）。Given a dataset with N total vectors, each vector is decomposed into M sub-vectors, where each sub-space has a dimension of d/M. While the lengths of these sub-vectors don’t have to be exactly the same, it is recommended to use the same length for ease of code implementation.
        • 对数据集中所有子向量使用 k-均值（或其他聚类算法）。这会为每个子空间给出一组 K 个质心，每个质心都将被分配其唯一的 ID。Apply the k-means algorithm (or any other clustering algorithm) to all the sub-vectors in the dataset. This will provide a set of K centroids for each sub-space, and each centroid will be assigned a unique ID.
        • 在计算出所有质心后，我们将用其最近质心的 ID 替换原始数据集中的所有子向量。replace all the original sub-vectors in the dataset with the ID of their nearest centroid.
        • 给定一个新的 d dimension 的向量，分成 M 个子向量，分别对应每个子向量找到对应的质心，然后用质心 ID 组合起来。Given a new d-dimensional vector, divide it into M sub-vectors, each corresponding to a sub-space. Find the corresponding centroid for each sub-vector and combine them using the centroid IDs.

除暴力搜索能精确索引到近邻，所有搜索算法只能在性能、召回率、内存三者 进行权衡。

IVF-PQ

• IVF-PQ **索引涉及附加参数: ** 1. 搜索算法向外扩展至参数指定中心数量 n_probes

• PQ 子向量数量和 IVF 分区数量的平衡，才能有效构建 IVF-PQ 索引:

  1. 1)PQ 子向量越多，子空间越小，导致信息失真;2)子向量多会导致 PQ 步骤中 I/O 和计算量增加。
  2. 控制 IVF 分区数以平衡召回和搜索速度。分区数量 = 向量数量 »> 暴力搜索，沦为 IVF-Flat 索引。

支持索引总结

在搜索或查询插入的向量前，必须声明索引类型和相似度度量。索引类型:

  1. FLAT:适合在小规模，百万级数据集上寻求完全准确和精确的搜索结果的场景。
  2. I VF_FL A T:适合于在精度和查询速度之间寻求理想平衡的场景。
  3. I VF_SQ:适合于在磁盘、CPU和GPU内存消耗非常有限的场景中显著减少资源消耗。
  4. I VF_PQ:适合于在高查询速度的情况下以牺牲精度为代价的场景。
  5. HNS W:基于图形的索引，最适合于对搜索效率有很高需求的场景。

HNSW

参考

Hierarchical Navigable Small Worlds

HNSW 在查询速度和准确度上有非常好的平衡，也因此成为最受欢迎的 vector search 的算法。要学习 HNSW，需要先熟悉两个概念，skip-list（跳表）和 Navigable Small Worlds (NSW)。

Skip-List（跳表）

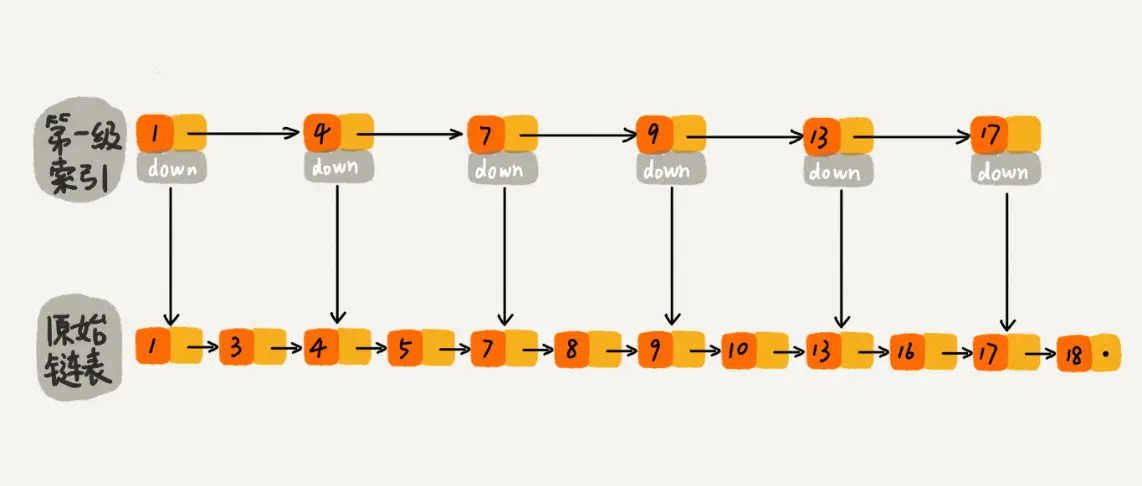
Skip List–跳表

先在索引找 1、4、7、9，遍历到一级索引的 9 时，发现 9 的后继节点是 13，比 10 大，于是不往后找了，而是通过 9 找到原始链表的 9，然后再往后遍历找到了我们要找的 10，遍历结束。有没有发现，加了一级索引后，查找路径：1、4、7、9、10，查找节点需要遍历的元素相对少了，我们不需要对 10 之前的所有数据都遍历，查找的效率提升了。

img

那如果加二级索引呢？这就是跳表的思想，用“空间换时间”，通过给链表建立索引，提高了查找的效率。

当数据量足够大时，效率提升会很大。使得链表能够实现二分查找。由此可以看出，当元素数量较多时，索引提高的效率比较大，近似于二分查找。跳表是可以实现二分查找的有序链表。

假如一直往原始列表中添加数据，但是不更新索引，就可能出现两个索引节点之间数据非常多的情况，极端情况，跳表退化为单链表，从而使得查找效率从 O(logn) 退化为 O(n)。

我们在原始链表中随机的选 n/2 个元素做为一级索引是不是也能通过索引提高查找的效率呢？当原始链表中元素数量足够大，且抽取足够随机的话，我们得到的索引是均匀的。

所以，我们可以维护一个这样的索引：随机选 n/2 个元素做为一级索引、随机选 n/4 个元素做为二级索引、随机选 n/8 个元素做为三级索引，依次类推，一直到最顶层索引。这里每层索引的元素个数已经确定，且每层索引元素选取的足够随机，所以可以通过索引来提升跳表的查找效率。

首先想象一个网络，网络上有许多节点，这些节点有些相互联通。每个节点会和联通的节点有短距离、中距离或者长距离的连接。

在执行搜索时，我们将从某个预先设定的的入口点开始搜索。从那里，我们通过比较搜索点和这个点以及其联通的点的距离，并跳转到距离搜索点节点最近的节点。这个过程重复，直到我们找到最近的邻居。这种搜索称为贪心搜索。这个算法适用于数百或数千个节点的小型 NSW，但对于更大的 NSW 则效率比较低。一个优化方法是通过增加每个节点的短距离、中距离和长距离连接的节点的数量，但这会增加网络的整体复杂性，并导致搜索时间变长。

将向量数据集中的所有向量想象成 NSW 中的点，

长距离连接的点表示彼此不相似的两个向量 （提高搜索效率）

短距离连接的点则相反，表示两个近似的向量。（提高搜索精度）

通过这种方式，将整个数据集向量构建成 NSW，我们可以通过贪婪算法遍历 NSW，朝着越来越接近搜索向量的顶点方向移动，完成近邻搜索。

HNSW 的查询和构建

从上往下，从长边到短边搜索

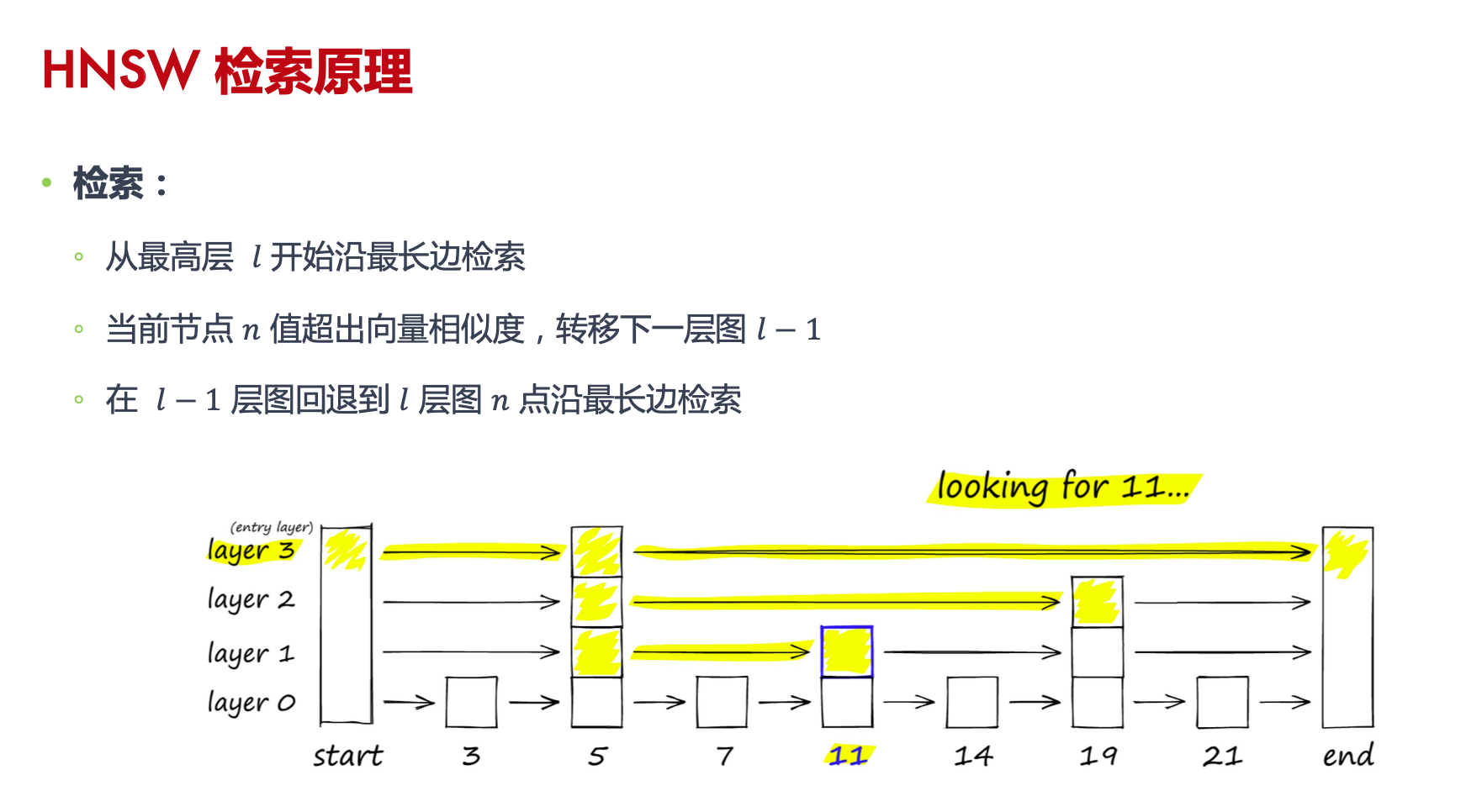
image-20240215223716808

诞生了结合跳表和 NSW 的 HNSW：与跳表一样，HNSW 是一个多层级的数据结构，每层不是链表，而是由 NSW 构成

img

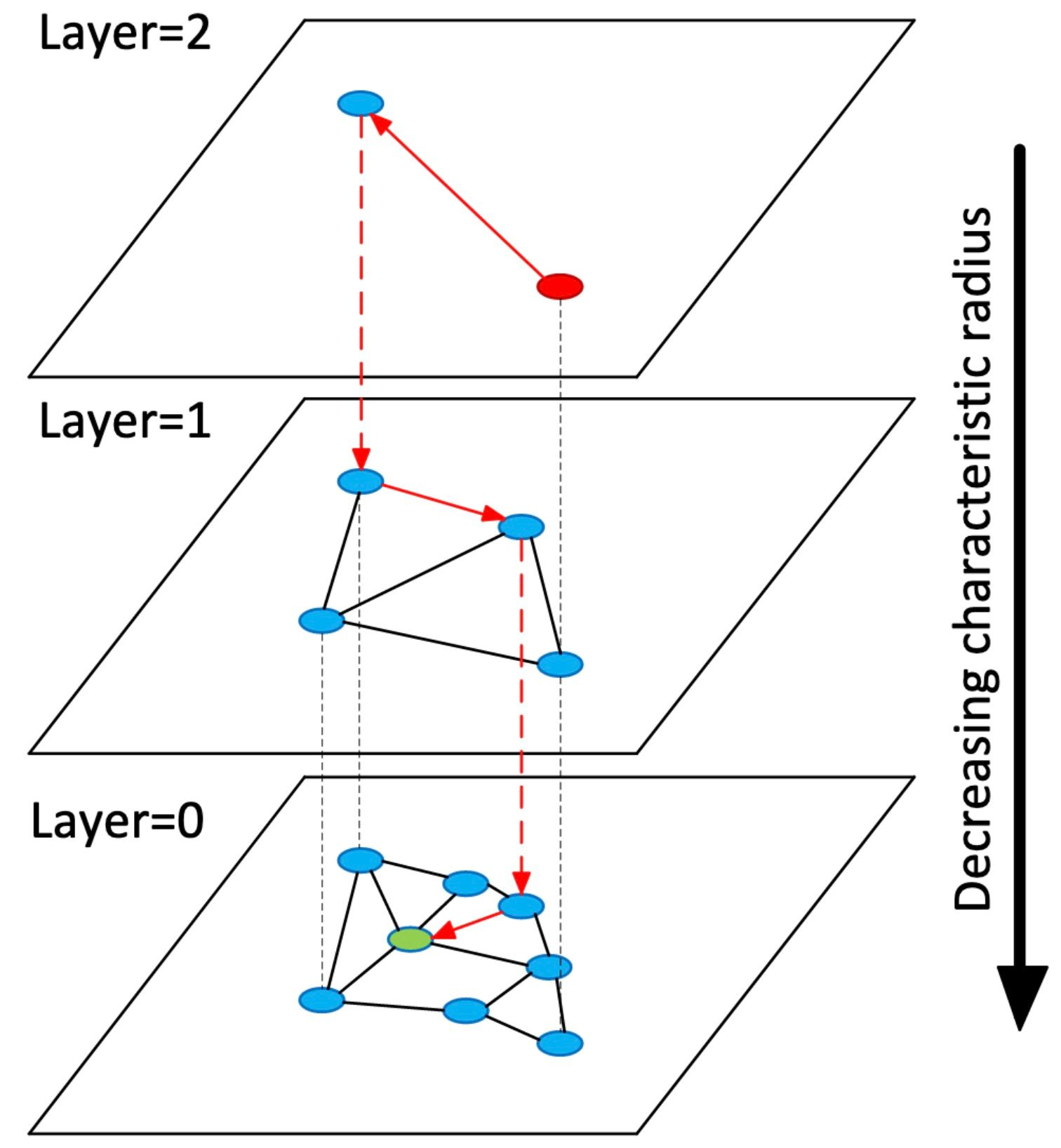
HNSW 图的最上层有很少的节点，且节点间的距离都很长。而最底层则包括所有节点和最短的链接。搜索过程如下：给定一个查询向量，我们先进入最上层的一个预定义的搜索起点，并通过贪婪算法朝着与我们的查询向量最近的邻居方向前进。一旦到达最近的节点，我们就在第二层重复此过程。这个过程一直持续到最底层，直到我们找到最近的邻居节点，搜索结束。

HNSW 的另一个优势，区别于我们已经学习过的其他向量存储方式，就是更高效地支持插入新的向量。插入操作和跳表的插入操作类似。对于某个向量 v，我们先通过搜索算法，找到这个向量在最底层的位置：

  • 首先遍历图的第一层，找到它的最近邻居，然后移到其下方的层次；然后，再次遍历图，以在第二层找到它的最近邻居；这个过程一直持续，直到在最底层的图中找到最近的邻居。
  • 第二步，需要确定向量 v 和哪些现有节点建立连接（顶点之间的连接）。通常会设定一个预定义的参数 M，它决定了我们可以添加的双向链接的最大数量。这些链接通常设置为 v 的最近邻居。与跳表一样，查询向量在上层出现的概率呈指数递减，可以试用一个随机函数来判断是否要创建上层的节点。

算法参数

相同数量级的数据集，维度越大，RAM占用越大，搜索时间越长。

  • M在构造过程中为每个新元素创建的双向链接的数量。（在建表期间每个向量的边数目）

    M的合理范围在[2,200]。M越高，对于本身具有高维特征的数据集来讲，recall可能越高，性能越好；M越低，对于本身具有低维特征的数据集来讲，性能越好。M值决定了算法内存消耗。

    建议M：12，16，32。因为特征已经选择过了，维度一般不会太高。

  • efConstruction最近邻居的动态列表的大小（在搜索期间使用）。

    efConstruction 越大，构造时间越长，index quality越好。有时，efConstruction 增加的过快并不能提升index quality。有一种方法可以检查efConstruction 的选择是否可以接受。计算recall，当ef=efConstruction ，在M值时，如果recall低于0.9，那么可以适当增加efConstruction 的数值。

  • num_elements: 在index最大的元素个数。
  • ef: 动态检索链表的大小。当ef设置的越大，越准确同时检索速度越慢，ef不能设置的比检索最近邻的个数K小。ef的值可以设置为k到集合大小之间的任意值。
  • k: 结果中返回的最近邻的结果的个数k。knn_query函数返回两个numpy数据。分别包括k个最近邻结果的标签和与这k个标签的距离。

优化

  • 分段创建几个索引库，同时搜索，取距离值最小的作为最终的结果。
  • 加入了pca降维。主要原因是数据集很大，搜索时间过长，加上精度不理想（不相似的与相似的区分不开）。将特征从1280降到了128。

距离度量总结

9个数据科学中常见距离度量总结以及优缺点概述

用于衡量向量间相似性。好的距离度量方法可以显著提高向量分类和聚类性能。

浮点Embedding，通常使用欧氏距离和内积

  • 欧氏距离(L2):常用于计算机视觉领域(C V)
  • 余弦(Cos):常用于自然语言处理领域(NLP)。
  • 内积(IP):常用于自然语言处理领域(NLP)。

二元Embedding，广泛使用度量标准

  • 汉明距离:常用于自然语言处理领域(NLP)

浮点Embedding

内积

image-20240219103307657

优点:它简单易懂，计算速度快，兼顾向量长度和方向。

场景:适用图像识别、语义搜索和文档分类等。

问题:对向量长度敏感，计算高维向量相似性时会丢失信息

欧氏距离 Euclidean Distance

从最常见的距离度量开始，即欧几里得距离。最好将距离量度解释为连接两个点的线段的长度。

image-20230827192503090

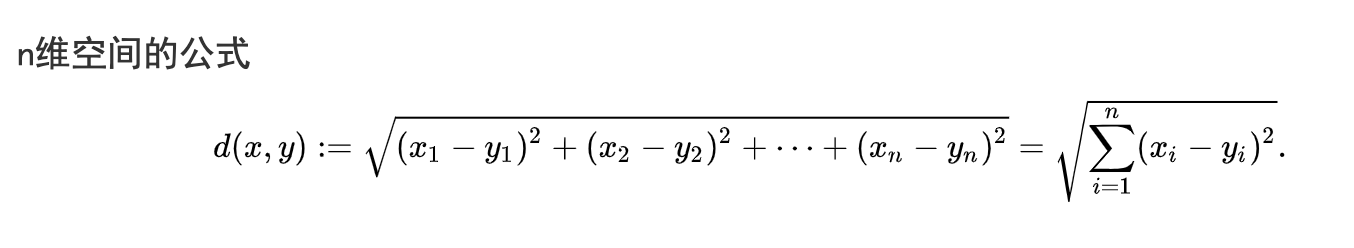
image-20230827192126871

尽管这是一种常用的距离度量，但欧几里德距离并不是比例不变的，这意味着所计算的距离可能会根据要素的单位而发生偏斜。通常，在使用此距离度量之前，需要对数据进行标准化。

缺点

此外，随着数据维数的增加，欧氏距离的用处也就越小。这与维数的诅咒有关，维数的诅咒与高维空间不能像期望的二维或三维空间那样起作用。

优点

您拥有低维数据并且向量的大小非常重要时，欧几里得距离的效果非常好。

余弦相似度 Cosine Similarity

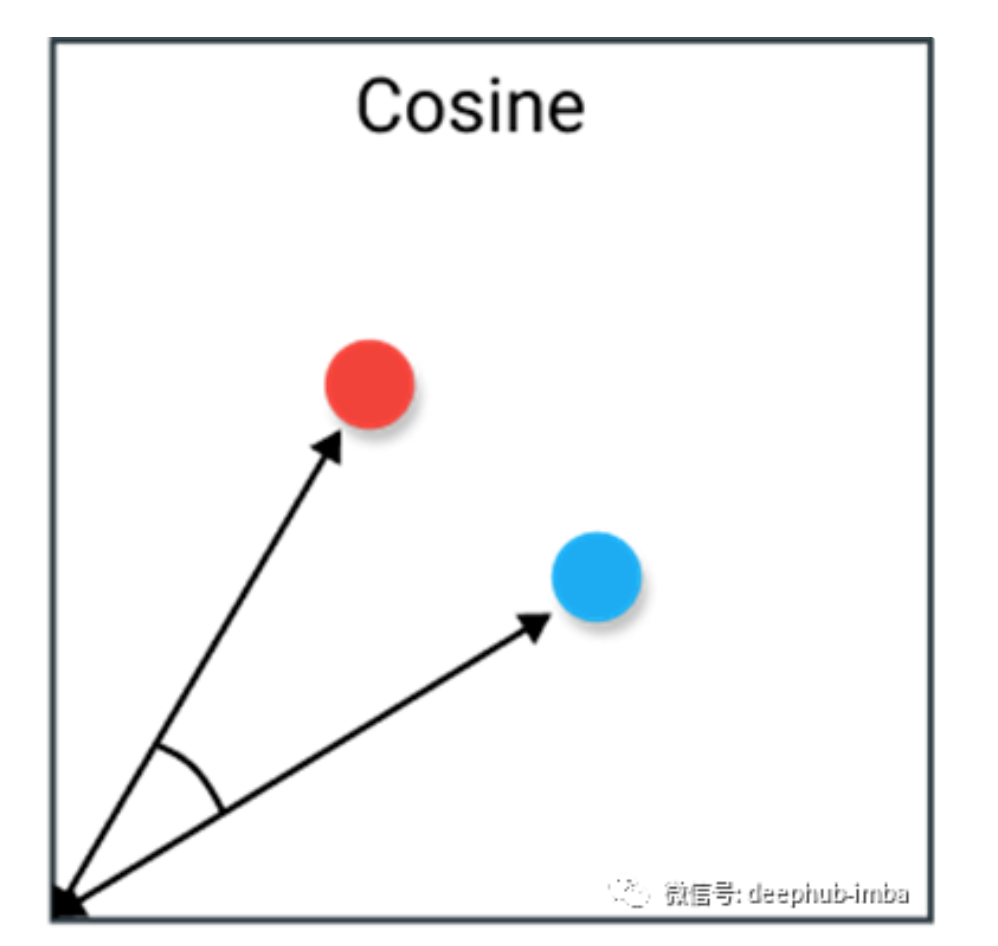
image-20230827192757565

余弦相似度经常被用作解决高维数欧几里德距离问题的方法。余弦相似度就是两个向量夹角的余弦。如果将向量归一化为长度均为1，则向量的内积也相同。

image-20230827193146224

缺点：

余弦相似度的一个主要缺点是没有考虑向量的大小，而只考虑它们的方向

优点：

当我们对拥有的高维数据向量的大小不关注时，通常会使用余弦相似度。对于文本分析，当数据由字数表示时，此度量非常常用。例如，当一个单词在一个文档中比另一个单词更频繁出现时，这并不一定意味着一个文档与该单词更相关。可能是文件长度不均匀，计数的重要性不太重要。然后，我们最好使用忽略幅度的余弦相似度。

二元Embedding

汉明距离 Hamming Distance

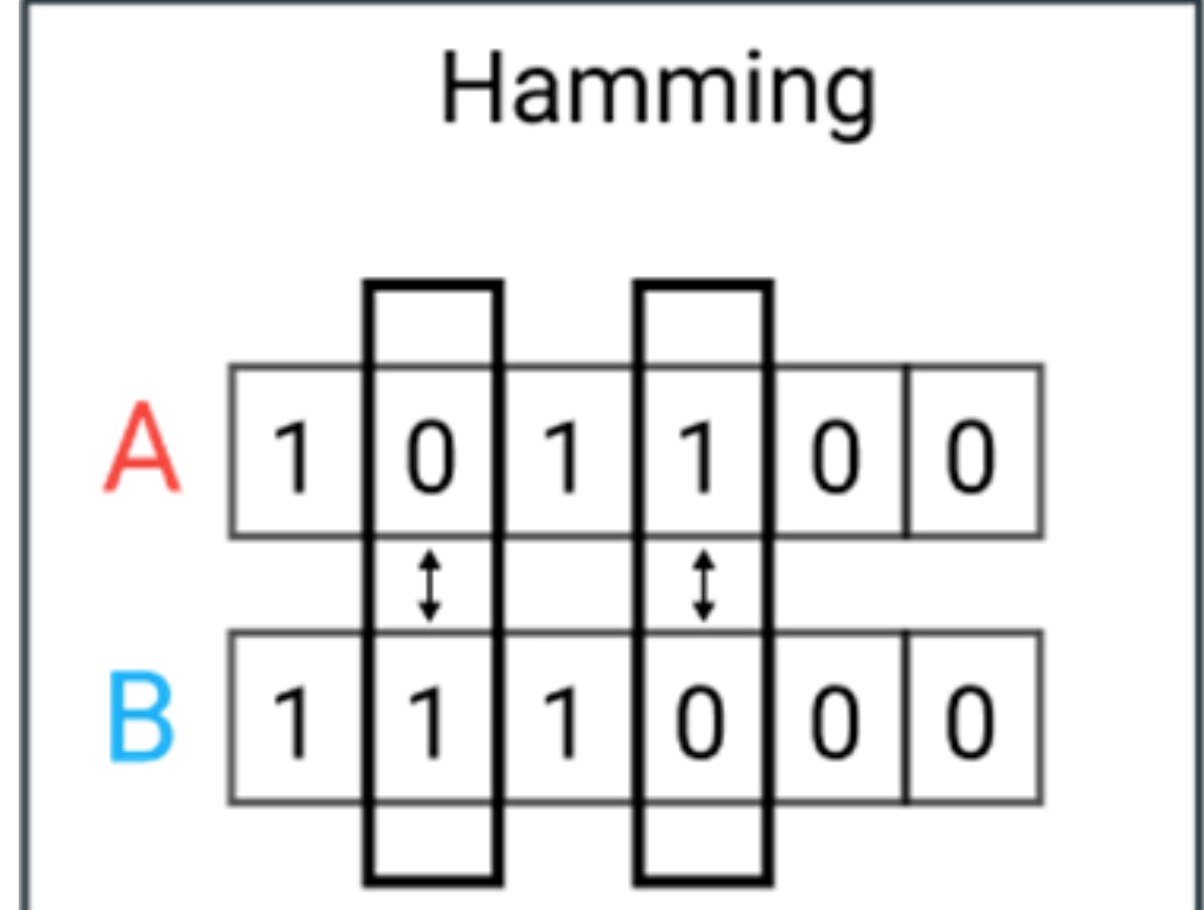
image-20230827194435739

汉明距离是两个向量之间不同值的个数。它通常用于比较两个相同长度的二进制字符串。它还可以用于字符串，通过计算不同字符的数量来比较它们之间的相似程度。

缺点

当两个向量的长度不相等时，很难使用汉明距离。为了了解哪些位置不匹配，您可能希望比较相同长度的向量。此外，只要它们不同或相等，就不会考虑实际值。因此，当幅度是重要指标时，建议不要使用此距离指标。

优点

典型的用例包括数据通过计算机网络传输时的错误纠正/检测。它可以用来确定二进制字中失真的数目，作为估计误差的一种方法。

曼哈顿距离 Manhattan Distance

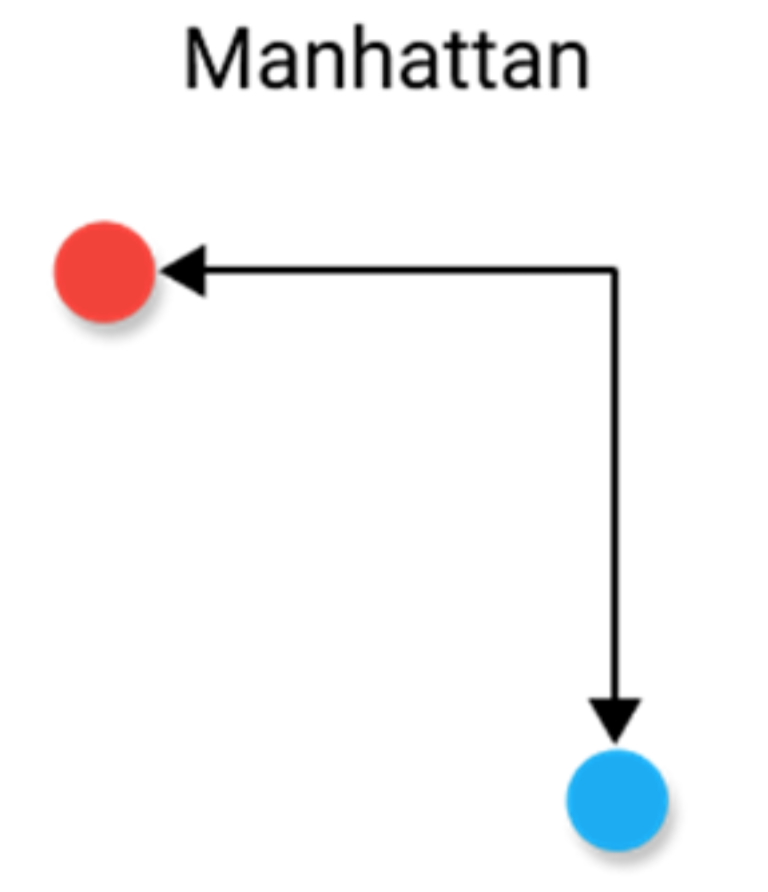
image-20230827195211837

曼哈顿距离，通常称为出租车距离或城市街区距离，计算实值向量之间的距离。想象描述均匀网格(如棋盘)上物体的向量。曼哈顿距离是指两个矢量之间的距离，如果它们只能移动直角。在计算距离时不涉及对角线移动。

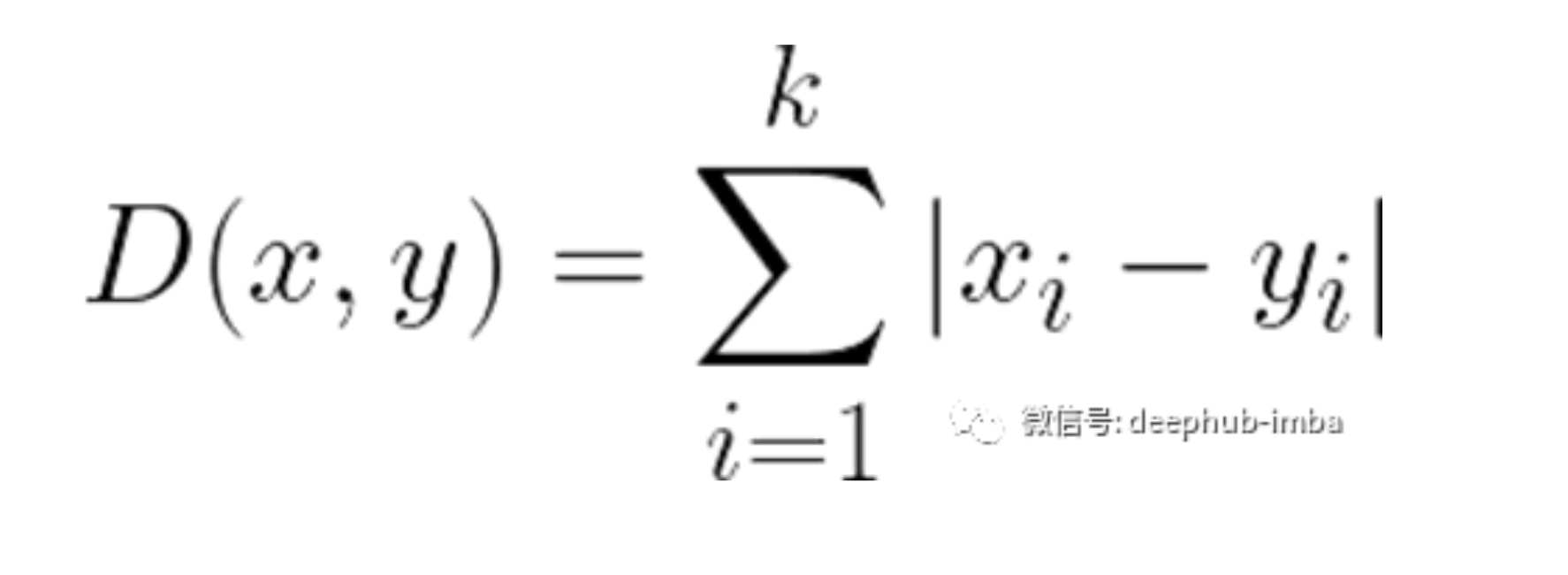
image-20230827195826282

缺点

曼哈顿距离在高维数据中似乎可以工作，但它比欧几里得距离更不直观，尤其是在高维数据中使用时。

优点

当数据集具有离散和/或二进制属性时，Manhattan似乎工作得很好，因为它考虑了在这些属性的值中实际可以采用的路径。以欧几里得距离为例，它会在两个向量之间形成一条直线，但实际上这是不可能的。

切比雪夫距离 Chebyshev Distance

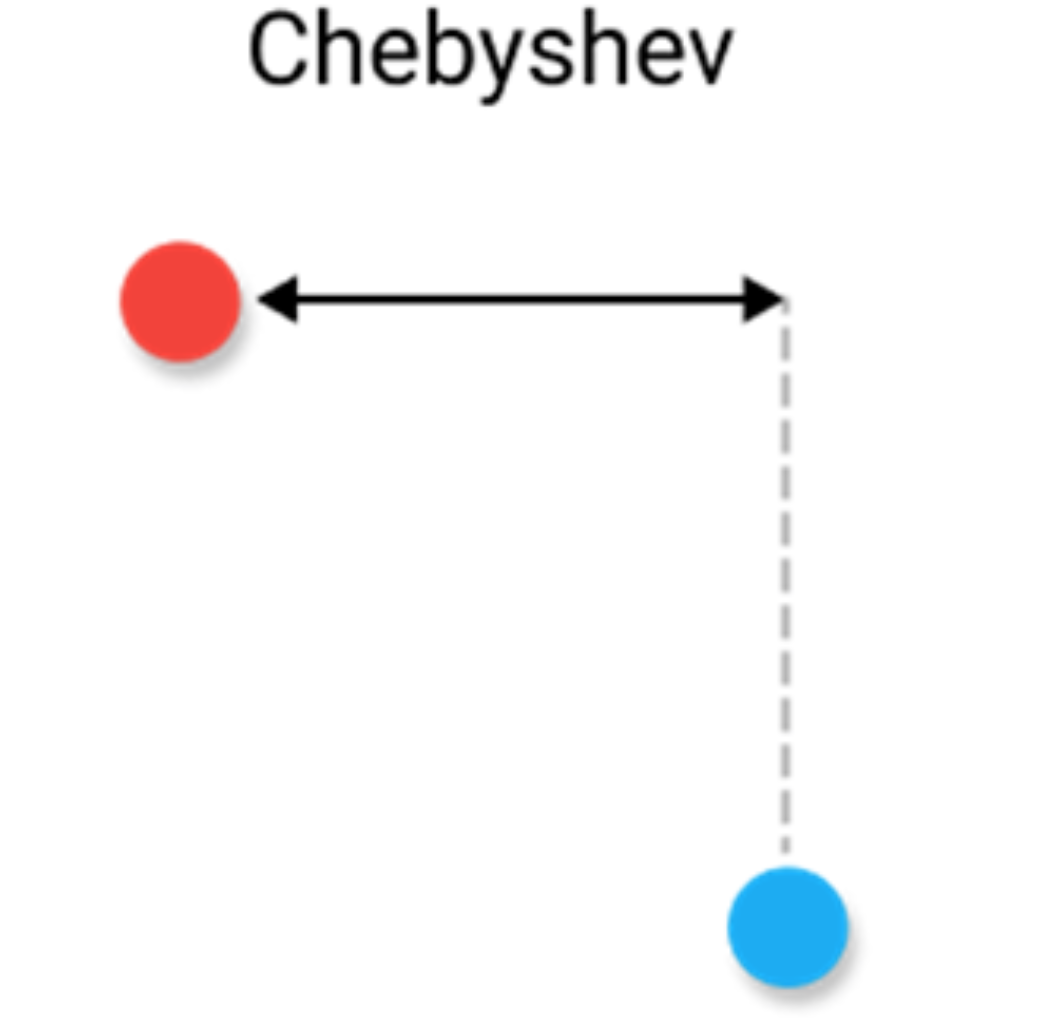
image-20230827200918300

切比雪夫距离定义为两个向量在任意坐标维度上的最大差值。换句话说，它就是沿着一个轴的最大距离。由于其本质，它通常被称为棋盘距离，因为国际象棋的国王从一个方格到另一个方格的最小步数等于切比雪夫距离。

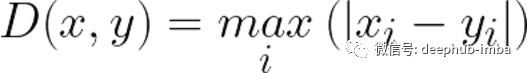
image

缺点

这使得它很难像欧氏距离或余弦相似度那样作通用的距离度量，因此，建议您只在绝对确定它适合您的用例时才使用它。

优点

切比雪夫距离可用于提取从一个正方形移动到另一个正方形所需的最小移动次数。此外，在允许无限制八向移动的游戏中，这可能是有用的方法。切比雪夫距离经常用于仓库物流，因为它非常类似于起重机移动一个物体的时间。

元数据过滤

参考

参考

进行相似性搜索前 or 后执行元数据过滤，Vector-DB 一般维护两个索引:

  • 向量索引 Vector Indexing
  • 元数据索引 Meta Indexing

实际业务场景，不需整 Vector-DB 相似性搜索，而通过部分业务字段进行过滤 Filtering 再查询。 存储在 Vector-DB 向量还需包含元数据 Mate Data，e.g. User ID、Doc ID 等信息。

优点:搜索时，根据元数据来过滤搜索结果，减少向量检索范围。

缺点:会导致 Vector-DB 查询过程变慢。

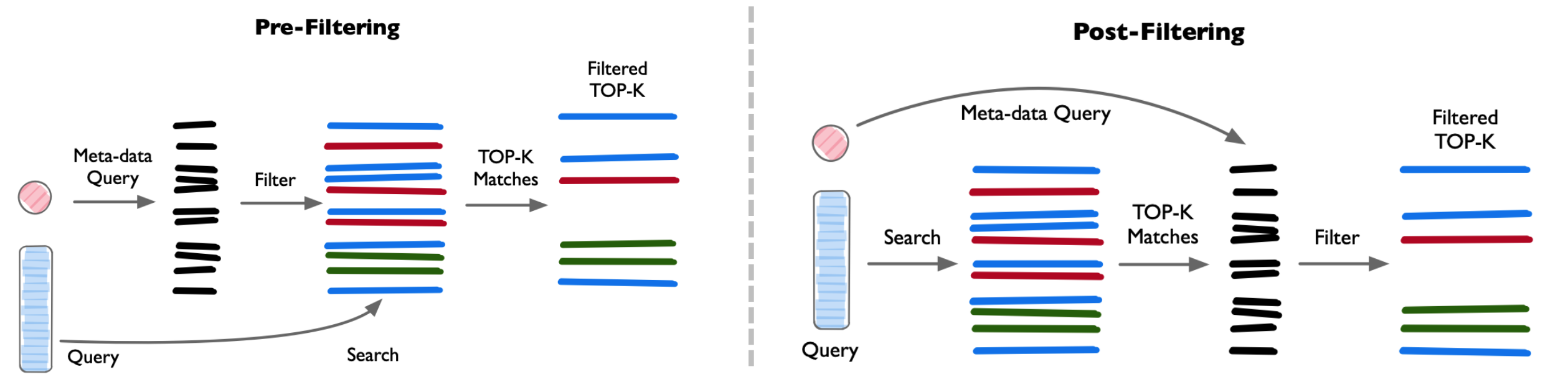
image-20240219105227876

  • Pre-filtering向量搜索前进行 Meta-data 过滤。可以减少搜索空间，但也可能导致系统忽略与 Meta-data 筛选标准不匹配的相关结果。
  • Post-filtering:向量搜索完后进行 Meta-data 过滤。可以确保考虑所有相关结果，搜索完成后将不相关结果进行筛选。

优化

  • 利用索引算法处理 Meta-data 或使用并行算法来加速过滤任务。
  • 平衡搜索性能和筛选精度，这对提供高效且相关查询结果至关重要。

性能

image-20240219112724416

Vector-DB 典型检索场景

  • 搜索推荐:大量用户并发查询(高QPS)，对查询延时非常敏感(<100ms)
  • 大规模向量检索:e.g. 门禁、人脸，海量向量持久化存储，快速检索延时敏感(<1s)
  • 大模型推理:单次查询较多，查询时延敏感;单个任务 QPS 相对较低

衡量

  • 插入速度更重要，还 是查询速度更重要
  • 应用是否满足业务查 询时的延迟
  • 召回率和延迟间作取舍