线性模型

发表于 | 分类于 | 阅读次数

线性回归假设

Regression Analysis with Assumptions, Plots & Solutions

Linearity 线性

应变量和每个自变量都是线性关系。

非线性/不满足可加性 模型将无法很好的描述变量之间的关系，极有可能导致很大的泛化误差（generalization error）

Indpendence 独立性

误差项

对于所有的观测值，它们的误差项相互之间是独立的。

自相关性（Autocorrelation）经常发生于时间序列数据集上，后项会受到前项的影响。如果误差项是相关的， 则估计的标准差倾向于 < 真实的标准差。置信区间和预测区间变窄。较窄的置信区间意味着95％置信区间的概率小于0.95，它将包含系数的实际值。 Durbin – Watson (DW)它必须介于0和4之间。如果DW = 2，则表示没有自相关，0 <DW <2表示正自相关，而2 <DW <4表示负自相关。

自变量之间应相互独立

当发现自变量是中度或高度相关时,多重共线性,会导致我们测得的标准差偏大，置信区间变宽。

VIF因子 VIF<=4 没有多重共线性 VIF>=10 严重的多重共线性。

最小二乘法的基础上，加入了一个与回归系数的模有关的惩罚项（岭回归，Lasso回归或弹性网（ElasticNet）回归），可以收缩模型的系数。一定程度上减少方差。

Normality 正态性

误差项服从正态分布,均值为0。

如果误差项不呈正态分布，需要重点关注一些异常的点（误差较大但出现频率较高）

Equal-variance 等方差

所有的误差项具有同样方差。为常数。

异方差性，出现在有异常值（Outlier）的数据集上，对模型影响很大。

普通线性回归模型

目标函数 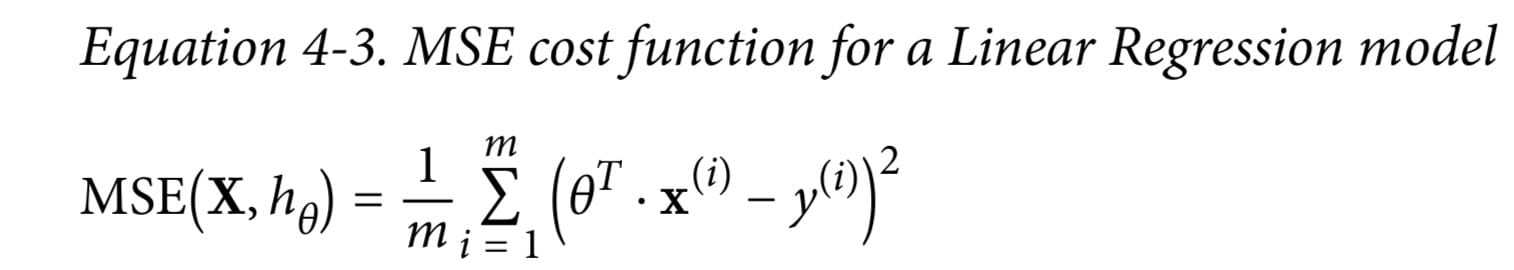最小二乘法求权重 

1
2
3
4
5
6
7
>>> from sklearn.linear_model import LinearRegression
>>> lin_reg = LinearRegression()
>>> lin_reg.fit(X,y)
>>> lin_reg.intercept_, lin_reg.coef_
(array([4.21509616]),array([2.77011339]))
>>> lin_reg.predict(X_new)
array([[4.21509616],[9.75532293]])

logistic 分类

二元分类logistic

预测值表示为1的概率，取值范围在[0,1]之间

\[h=P(y=1 | x)\]

$ŷ=w^Tx+b$普通回归模型套一个 sigmoid function 控制输出 (0,1)

\[ŷ=Sigmoid(w^Tx+b)\] \[Sigmoid(z)=\frac1{1+e^{-z}}\] \[L(ŷ ,y)=−(ylog ŷ +(1−y)log (1−ŷ ))\]

Cost function

\[J(w,b)=\frac1m\sum_{i=1}^m\;L(\;\widehat y^{(i)}\;,y^{(i)})\;=\;-\frac1m\sum_{i=1}^m\lbrack y^{(i)}\log\;\;\widehat y^{(i)}+(1-\;y^{(i)})\log\;(1-\;\widehat y^{(i)}\;)\rbrack\] 
1
2
3
4
5
6
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> list(iris.keys())
['data', 'target_names', 'feature_names', 'target', 'DESCR']
>>> X = iris["data"][:, 3:] # petal width
>>> y = (iris["target"] == 2).astype(np.int)

逻辑回归模型也可以 $\ell_1$ 或者 $\ell_2$ 惩罚使用进行正则化。Scikit-Learn 默认添加了 $\ell_2$ 惩罚。

1
2
3
4
5
6
7
8
9
10
from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(X, y)

# 如果你使用它进行预测（使用predict()方法而不是predict_proba()方法），它将返回一个最可能的结果
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", label="Iris-Virginica")
plt.plot(X_new, y_proba[:, 0], "b--", label="Not Iris-Virginica")

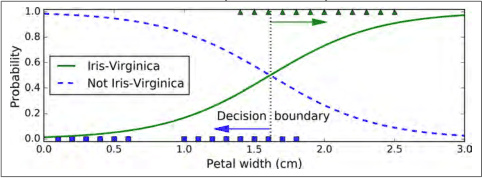
在 Scikit-Learn 的LogisticRegression模型中控制正则化强度的超参数不是 $\alpha$（与其他线性模型一样），而是它的逆：C。 C 的值越大，模型正则化强度越低。

多类别分类 softmax

Logistic 回归模型可以直接推广到支持多类别分类

1
2
3
def softmax(X):
    exps = np.exp(X)
    return exps / np.sum(exps)

softmax 损失函数 cross entry 

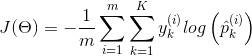
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def cross_entropy(X,y):
    """
    X is the output from fully connected layer (num_examples x num_classes)
    y is labels (num_examples x 1)
    	Note that y is not one-hot encoded vector. 
    	It can be computed as y.argmax(axis=1) from one-hot encoded vectors of labels if required.
    """
    m = y.shape[0]
    p = softmax(X)
    # We use multidimensional array indexing to extract 
    # softmax probability of the correct label for each sample.
    # Refer to https://docs.scipy.org/doc/numpy/user/basics.indexing.html#indexing-multi-dimensional-arrays for understanding multidimensional array indexing.
    log_likelihood = -np.log(p[range(m),y])
    loss = np.sum(log_likelihood) / m
    return loss

交叉熵，应该导致这个目标，因为当它估计目标类别的低概率时，它会对模型进行惩罚。交叉熵通常用于衡量一组估计的类别概率与目标类别的匹配程度

目标函数 

1
2
3
4
5
6
7
8
9
10
X = iris["data"][:, (2, 3)] # petal length, petal width
y = iris["target"]

softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10)
softmax_reg.fit(X, y)

>>> softmax_reg.predict([[5, 2]])
array([2])
>>> softmax_reg.predict_proba([[5, 2]])
array([[ 6.33134078e-07, 5.75276067e-02, 9.42471760e-01]])

Gradient 梯度

梯度下降

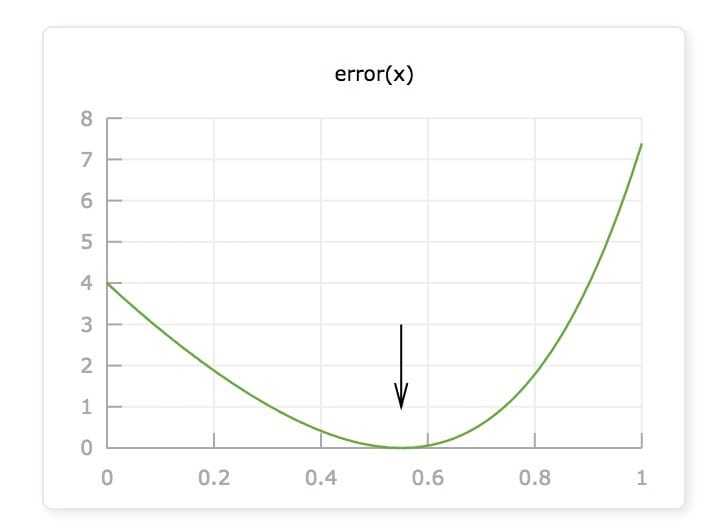error函数的图像，看上去像个碗一样，中间是凹的，两边翘起。这个碗的最低点，也就是 error(x) 的最小值，就是我们要寻找的点。

发现:

当x在最小值左边的时候，error函数的导数（斜率）是负的； 当x在最小值右边的时候，导数是正的； 当x在最小值附近的时候，导数接近0.

因此，如果我们在： 导数为负的时候增加x； 导数为正的时候减小x；

\[x = x - derivative * alpha\]

解释：

求权重的偏导

  • derivative 是 error 在 x 处的导数，这里是用导数的定义求的。 x = x - derivative 这就是“导数下降”名称的由来。通过不断地减去导数，x最终会到达函数的最低点。
  • alpha 参数控制的是点 x 逆着导数方向前进的距离（下降速度），alpha 越大，x 就会前进得越多，误差下降得越快。alpha 太小会导致下降缓慢，alpha 太大会导致 x 冲得太远，令函数无法收敛。

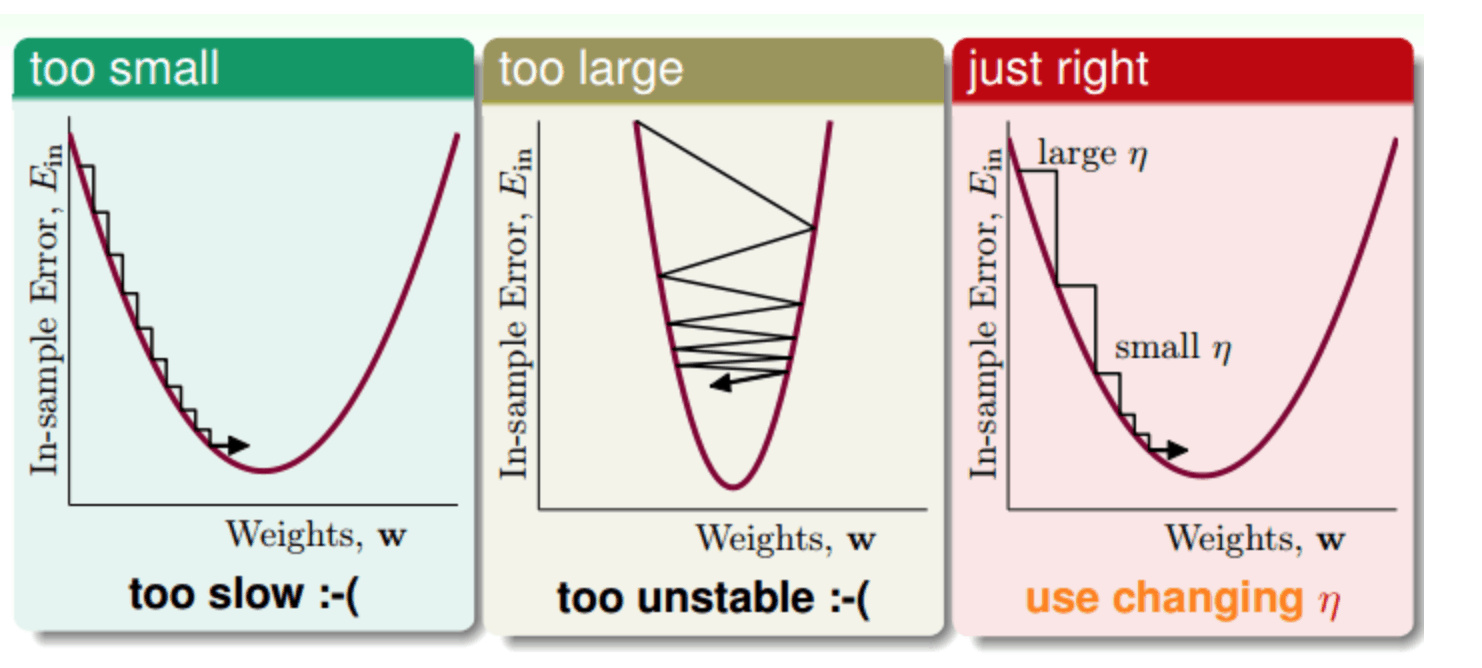
Batch Gradient Descent

它使用整个训练集来计算每一步的梯度，这使得训练集很大时非常缓慢

1
2
3
4
5
6
7
8
9
eta = 0.1 # 学习率
n_iterations = 1000
m = 100

theta = np.random.randn(2,1) # 随机初始值

for iteration in range(n_iterations):
    gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
    theta = theta - eta * gradiens

Stochastic Gradient Descent

随机梯度下降只是在每个步骤中在训练集中选取一个随机实例，并仅基于该单个实例计算梯度 由于其随机性，该算法比批处理梯度成本函数会上下反弹 只会平均减少 随着时间的推移， 它将最终接近最小值，但一旦它到达那里，它将继续反弹，永远不会稳定下来。 所以一旦算法停止，最终的参数值是好的，但不是最优的

当成本函数非常不规则时，这实际上可以帮助算法跳出局部最小值， 因此，随机性很好地摆脱局部最优。但不好，因为这意味着该算法永远无法最小化

方法是 逐渐降低学习率。这些步骤开始较大（这有助于快速进展并避免局部最小值）， 然后变得越来越小，从而使算法在全局最小值处达到最小。（simulated annealing模拟退火）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
n_epochs = 50
t0, t1 = 5, 50  #learning_schedule的超参数

def learning_schedule(t):
    return t0 / (t + t1)

theta = np.random.randn(2,1)

for epoch in range(n_epochs):
    for i in range(m):
        random_index = np.random.randint(m)
        xi = X_b[random_index:random_index+1]
        yi = y[random_index:random_index+1]
        gradients = 2 * xi.T.dot(xi,dot(theta)-yi)
        eta = learning_schedule(epoch * m + i)
        theta = theta - eta * gradiens

Mini-batch Gradient Descent

小批量的小随机实例集上的梯度

进展比SGD更不稳定，特别是在相当大的小批量时。 因此，小批量GD最终会走得比SGD更接近最小值。但另一方面，它可能难以摆脱局部最小值

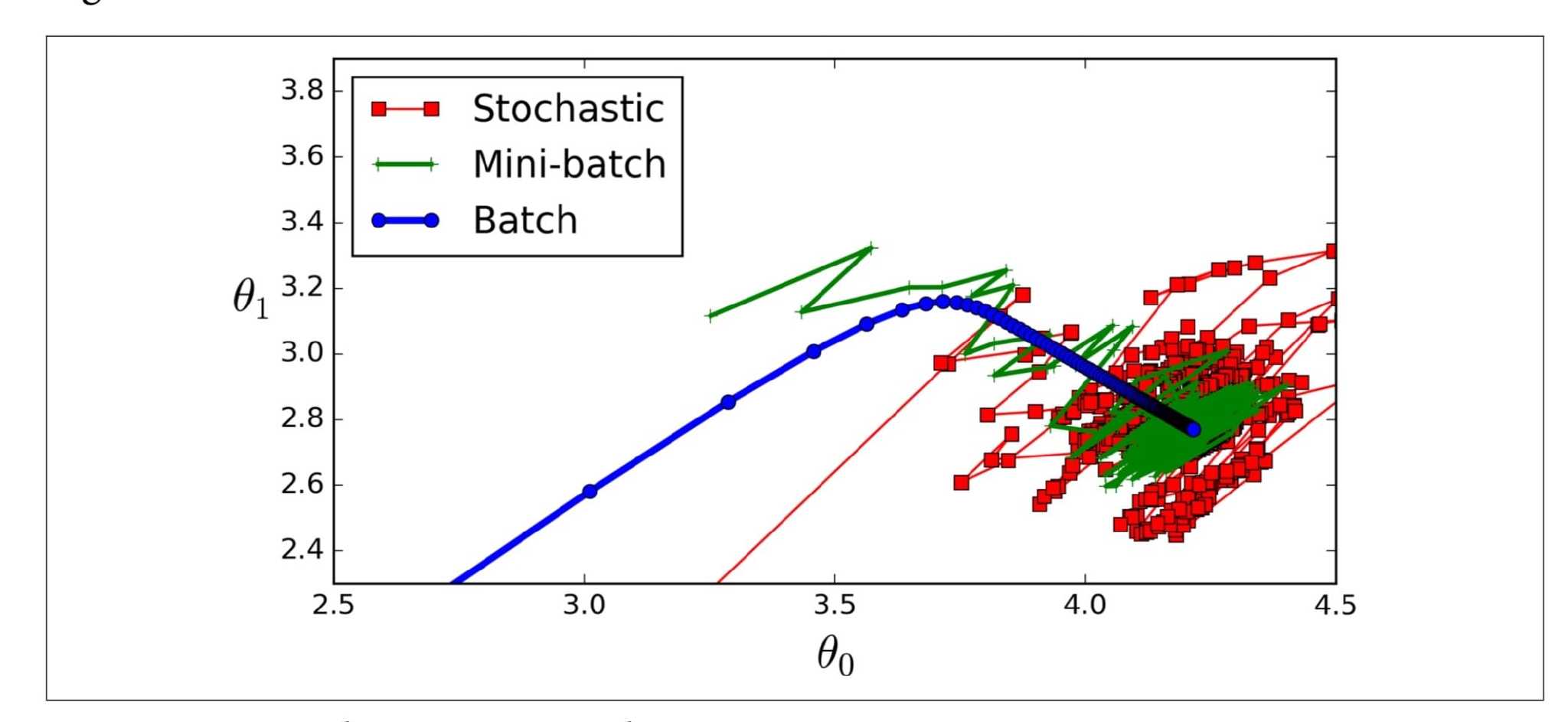
m is the number of training instances and n is the number of features

多项式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
m = 100
X = 6 * np.random.rand(m, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)

>>> from sklearn.preprocessing import PolynomialFeatures
>>> poly_features = PolynomialFeatures(degree=2,include_bias=False)
>>> X_poly = poly_features.fit_transform(X)
>>> X[0]
array([-0.75275929])
>>> X_poly[0]
array([-0.75275929, 0.56664654])

>>> lin_reg = LinearRegression()
>>> lin_reg.fit(X_poly, y)
>>> lin_reg.intercept_, lin_reg.coef_
(array([ 1.78134581]), array([[ 0.93366893, 0.56456263]]))

模型预测函数 $\hat{y}=0.56x_1^2+0.93x_1+1.78$

非线性变换

用不太复杂的model 解决非线性问题 通过非线性变换，将非线性模型映射到另一个空间，转换为线性模型，再来进行线性分类

  • 特征转换
  • 训练线性模型

例如

模型太复杂容易带来过拟合 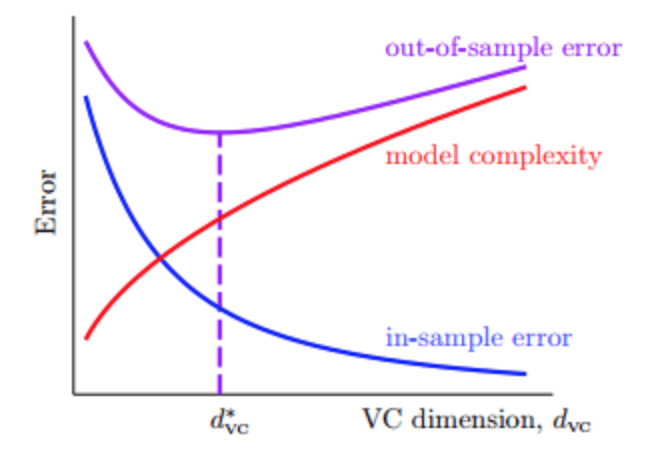非线性变换可能会带来的一些问题：时间复杂度和空间复杂度的增加，尽可能使用简单的模型，而不是模型越复杂越好

过拟合

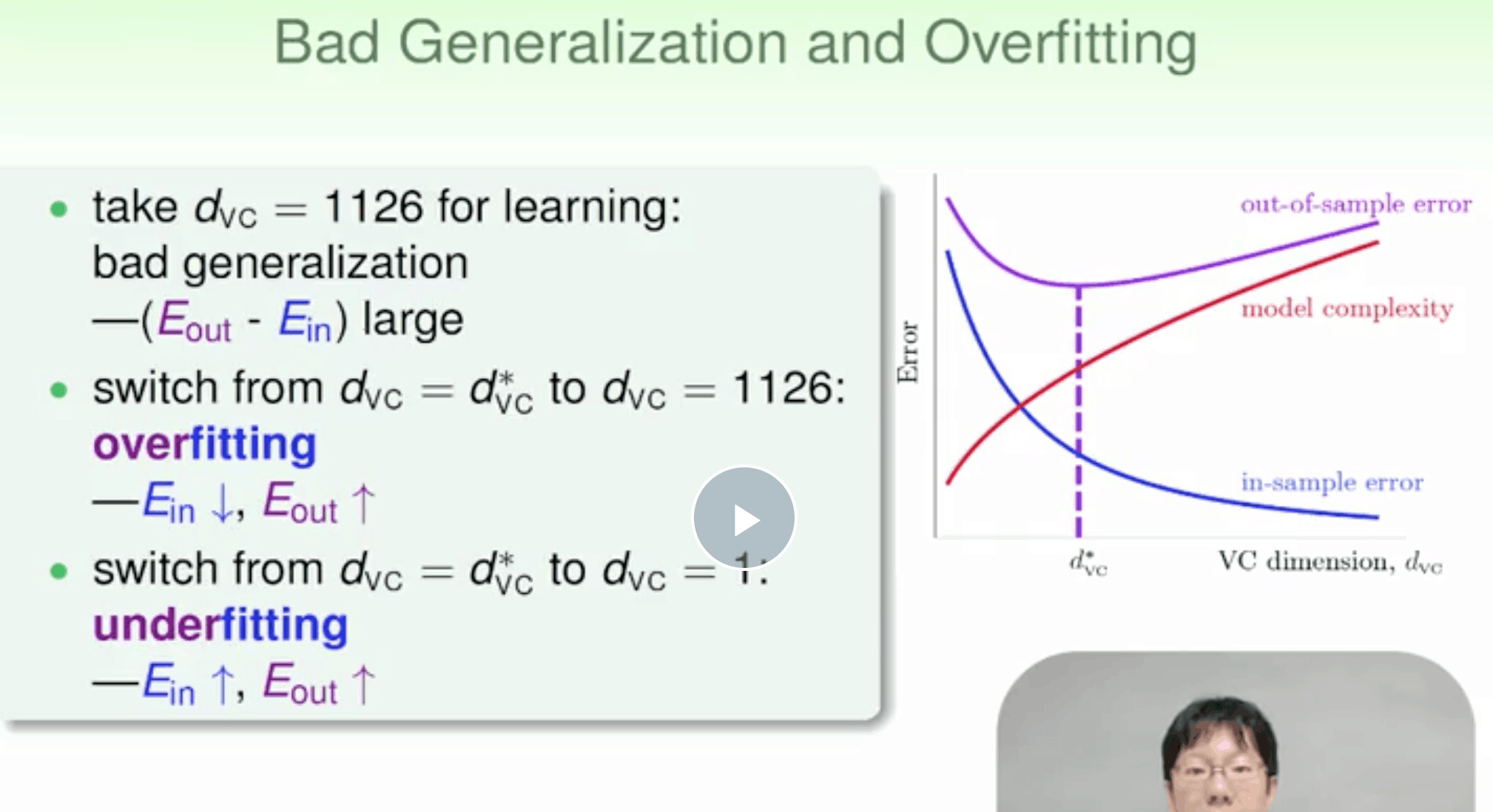
造成overfit 主要是

  • noise
  • 模型复杂度太高
  • train-set too small

    解决

  • 数据清洗（错误数据的更正，或者删除）
  • 简化模型
  • 更多数据 （如果没有办法获得更多的训练集，对已知的样本进行简单的处理、变换，从而获得更多的样本）
  • regularization
  • validation

维度灾难

当模型很复杂的时候 ，复杂度本身就会引入一种noise， 所以即使高阶无noise，模型也不能很好泛化。

Regularization

正则化 给予model惩罚 减低model复杂度。L1的在微分求导方面比较复杂。所以，一般L2 regularization更加常用

Ridge 岭回归 L2

普通回归+惩罚项（ $\alpha$ 越大惩罚越大）

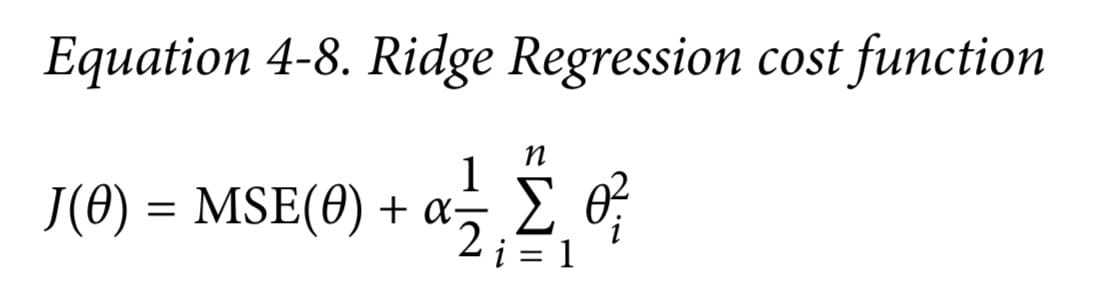
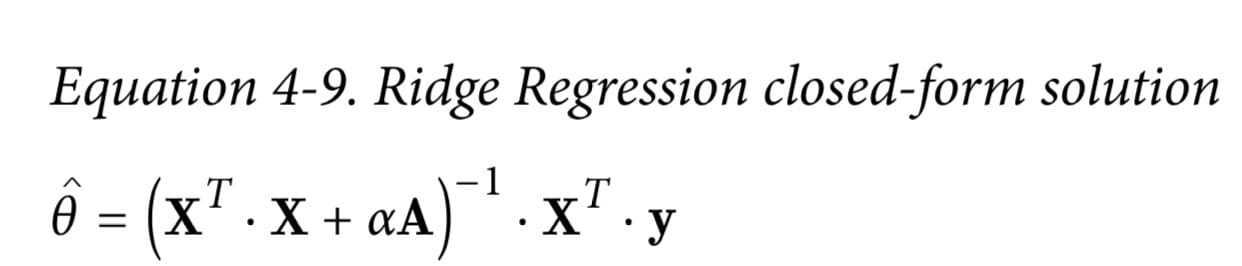
\[J(w,b)=\frac1m\sum_{i=1}^mL(\hat y^{(i)},y^{(i)})+\frac{\lambda}{2m}||w||_2^2\] \[||w||_2^2=\sum_{j=1}^{n_x}w_j^2=w^Tw\] 
1
2
3
4
5
>>> from sklearn.linear_model import Ridge
>>> ridge_reg = Ridge(alpha=1, solver="cholesky")
>>> ridge_reg.fit(X, y)
>>> ridge_reg.predict([[1.5]])
array([[ 1.55071465]]

1
2
3
4
>>> sgd_reg = SGDRegressor(penalty="l2")
>>> sgd_reg.fit(X, y.ravel())
>>> sgd_reg.predict([[1.5]])
array([[ 1.13500145]])

lasso L1

部分权重归0 完全消除最不重要的特征的权重

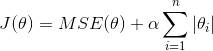
\[J(w,b)=\frac1m\sum_{i=1}^mL(\hat y^{(i)},y^{(i)})+\frac{\lambda}{2m}||w||_1\] \[||w||_1=\sum_{j=1}^{n_x}|w_j|\] 
1
2
3
4
5
6
7
8

SGDRegressor(penalty="l1")

>>> from sklearn.linear_model import Lasso
>>> lasso_reg = Lasso(alpha=0.1)
>>> lasso_reg.fit(X, y)
>>> lasso_reg.predict([[1.5]])
array([ 1.53788174]

弹性网络（ElasticNet）

弹性网络介于 Ridge 回归和 Lasso 回归之间。它的正则项是 Ridge 回归和 Lasso 回归正则项的简单混合，同时你可以控制它们的混合率 r，当 r=0 时，弹性网络就是 Ridge 回归，当 r=1 时，其就是 Lasso 回归。具体表示如公式 4-12。

公式 4-12：弹性网络损失函数 

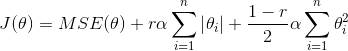
1
2
3
4
5
>>> from sklearn.linear_model import ElasticNet
>>> elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
>>> elastic_net.fit(X, y)
>>> elastic_net.predict([[1.5]])
array([ 1.54333232])

Ridge回归是一个很好的首选项，但是如果你的特征仅有少数是真正有用的，你应该选择 Lasso 和弹性网络。 就像我们讨论的那样，它两能够将无用特征的权重降为零。一般来说，弹性网络的表现要比 Lasso 好， 因为当特征数量比样本的数量大的时候，或者特征之间有很强的相关性时，Lasso 可能会表现的不规律。

早停法(Early Stopping)

随着迭代训练次数增加，train set error一般是单调减小的。而dev set error 先减小，之后又增大。发生了过拟合。 选择合适的迭代次数，即early stopping 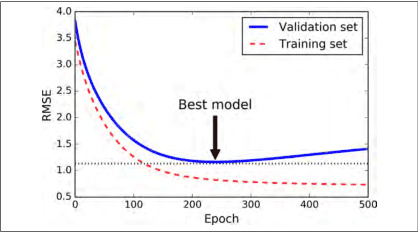只有在验证误差高于最小值一段时间后（你确信该模型不会变得更好了），才停止，之后将模型参数回滚到验证误差最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.base import clone

# 注意：当warm_start=True时，调用fit()方法后，训练会从停下来的地方继续，而不是从头重新开始。
sgd_reg = SGDRegressor(n_iter=1, warm_start=True, penalty=None,learning_rate="constant", eta0=0.0005)

minimum_val_error = float("inf")
best_epoch = None
best_model = None
for epoch in range(1000):
    sgd_reg.fit(X_train_poly_scaled, y_train)
    y_val_predict = sgd_reg.predict(X_val_poly_scaled)
    val_error = mean_squared_error(y_val_predict, y_val)
    if val_error < minimum_val_error:
        minimum_val_error = val_error
        best_epoch = epoch
        best_model = clone(sgd_reg)

更好的训练结果

  • 选择简单的model 参数很少，或者用regularization，数据集的特征减少中参数个数减少，都能降低模型复杂度
  • 训练数据和验证数据要服从同一个分布，最好都是独立分布的，这样训练得到的模型才能更好地具有代表性。
  • 在机器学习过程中，避免“偷窥数据”非常重要，但实际上，完全避免也很困难。实际操作中，有一些方法可以帮助我们尽量避免偷窥数据。第一个方法是“看不见”数据。就是说当我们在选择模型的时候，尽量用我们的经验和知识来做判断选择，而不是通过数据来选择。先选模型，再看数据。第二个方法是保持怀疑。就是说时刻保持对别人的论文或者研究成果保持警惕与怀疑，要通过自己的研究与测试来进行模型选择，这样才能得到比较正确的结论。